Вопросы, связанные с определением вычетов, были подробно разобраны в части 1 "Нахождение Вычетов". Методические указания по применению теории вычетов к нахождению ряда определенных интегралов, встречающихся в физических задачах, даны во второй и третьей частях.

Методами теории вычетов можно найти очень многие интегралы, но число приемов, употребляемых для этой цели, невелико. В п. 2.1 иллюстрируется метод сведения интеграла специального вида к контурному с помощью замены переменной интегрирования. В пп. 2.2- 2.5 показаны основные приемы вычисления интегралов в бесконечных пределах. Более сложные интегралы отнесены к третьей части. В пп. 3.1- 3.5 рассматриваются интегралы в полубесконечных пределах, а в пп. 3.6- 3.7 в конечных пределах. Все методы проиллюстрированы примерами. Классификация интегралов (пусть и несколько условная) облегчает усвоение материала. Студентам мы рекомендуем самостоятельно составлять "справочник" контуров интегрирования, используемых при вычислениях определенных интегралов.

Рассмотрим определенный интеграл

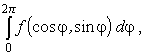
(1)

где f - рациональная функция. Интеграл типа (1) легко свести к интегралу по замкнутому контуру. Для этого сделаем замену, введя комплексную переменную z = e^ij При изменении j от 0 до 2p комплексная переменная z пробегает замкнутый контур - окружность |z| = 1 в положительном направлении. Интеграл (1) переходит в интеграл по замкнутому контуру от некоторой функции комплексной переменной. Условие рациональности f гарантирует, что получившаяся подынтегральная функция будет однозначной и аналитической, за исключением конечного числа полюсов. При этом только полюсы, попавшие внутрь контура |z| = 1 будут давать вклад в значение интеграла, вычисляемого по основной теореме вычетов.

В кеплеровой задаче период движения по эллиптической орбите с эксцентриситетом e 0 Ј e < 1 задается интегралом (размерный коэффициент отброшен)

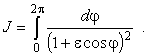
(2)

Положив z = e^ij получим dz = ie^ij ij или dj = dz/iz синус выразим по формуле Эйлера cosj = ( e^ij + e^{- ij} ) / 2 = ( z + 1/z ) / 2. Тогда интеграл (2) примет вид

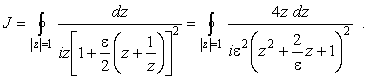
(3)

Особыми точками подынтегральной функции являются нули знаменателя

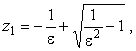
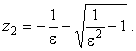
(4)

При заданных пределах изменения e только точка z₁ лежит внутри круга | z | < 1, тогда как | z₂ | > 1. Поэтому J = 2pi res ( z₁ ) Вычет в полюсе второго порядка z₁ легко рассчитать по формуле (12) части 1. Предварительно полезно разложить квадратный трехчлен на сомножители z + 2z / e + 1 = ( z - z )( z - z ) Тогда

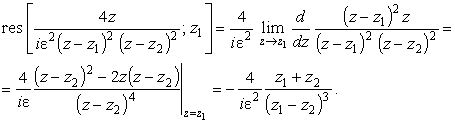
(5)

Подставив сюда z₁ и z₂ из (4), получим для интеграла

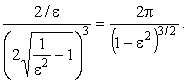
(6)

дальше