В третьей части даются методические указания по использованию контурного интегрирования для вычисления определенных интегралов в полубесконечных (п.п. 3.1-3.5) и конечных пределах (п.п. 3.6-3.7).
3.1. Интегралы от рациональных функций в полубесконечных пределах
Рассмотрим интеграл
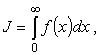
|
(1) |
где f(x) - рациональная функция, удовлетворяющая
лемме 1.
Для четных f(x) интеграл (1) равен
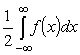 ,
и применим метод п.2.2.
Если же f(x) не является четной функцией, то можно воспользоваться двумя
способами, один из которых мы разберем сейчас, а другой отложим до п. 3.7. Первый способ прост,
но применим лишь к функциям специального вида; второй является общим методом, но более трудоемк.
,
и применим метод п.2.2.
Если же f(x) не является четной функцией, то можно воспользоваться двумя
способами, один из которых мы разберем сейчас, а другой отложим до п. 3.7. Первый способ прост,
но применим лишь к функциям специального вида; второй является общим методом, но более трудоемк.
|
Вычислим интеграл
|
||
|
Уравнение
zn + 1 = 0
имеет такие корни:
|
|
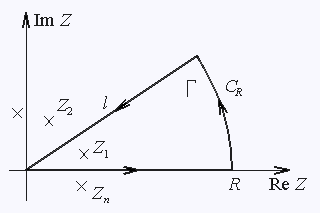
| Рис 1. | ||
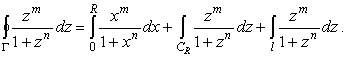
|
(2) |
Попытаемся выразить интеграл по отрезку l через интеграл
по действительной оси. Подставив
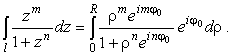
|
(3) |
Выберем
j0
так, чтобы
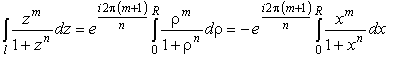
|
(4) |
и из (2) имеем
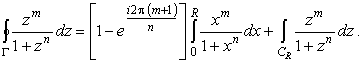
|
(5) |
Контурный интеграл в (5) может быть через
вычет в особой точке
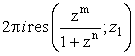 .
После предельного перехода
.
После предельного перехода
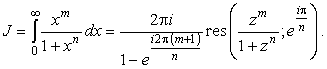
|
(6) |
Далее следует вычислить вычет и убедиться, что полученное выражение преобразуется к виду, не содержащему мнимой единицы, поскольку искомый интеграл действителен. Имеем
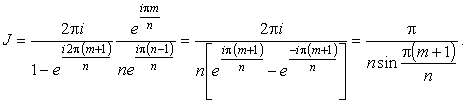
|
(7) |
очевидно, что этим методом можно пользоваться только при
интегрировании таких функций, которые на луче
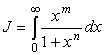 ,
где m, n - положительные целые числа и
,
где m, n - положительные целые числа и
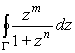 ,
где замкнутый контур Г (см. рис.1) состоит из трех частей:
отрезка [0, R] действительной оси, дуги CR
,
где замкнутый контур Г (см. рис.1) состоит из трех частей:
отрезка [0, R] действительной оси, дуги CR