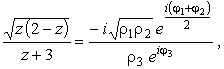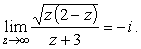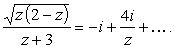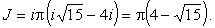Вычислим интеграл
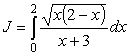 .
Здесь точки вставления при z = 0 и z = 2.
Соединим их разрезом и выберем, например, ту ветвь функции,
которая на верхнем берегу разреза принимает положительные
значения. Очевидно, на нижнем берегу разреза подынтегральная
функция будет отличаться лишь знаком. Поэтому интегралы по
верхнему и нижнему берегам в сумме дадут 2J. Интегралы по
окружностям
| z | = r
и
| z - 2 | = r
стремятся к нулю при
r ® 0 .
Это нетрудно показать, представив в одном случае
z = r
exp ( ij )
и
z - 2 = r
exp ( ij )
в другом. Основная теорема теории вычетов не применима к
области внутри Г, так как функция не аналитична на линии разреза.
Применяя теорему к области вне Г, получим
.
Здесь точки вставления при z = 0 и z = 2.
Соединим их разрезом и выберем, например, ту ветвь функции,
которая на верхнем берегу разреза принимает положительные
значения. Очевидно, на нижнем берегу разреза подынтегральная
функция будет отличаться лишь знаком. Поэтому интегралы по
верхнему и нижнему берегам в сумме дадут 2J. Интегралы по
окружностям
| z | = r
и
| z - 2 | = r
стремятся к нулю при
r ® 0 .
Это нетрудно показать, представив в одном случае
z = r
exp ( ij )
и
z - 2 = r
exp ( ij )
в другом. Основная теорема теории вычетов не применима к
области внутри Г, так как функция не аналитична на линии разреза.
Применяя теорему к области вне Г, получим
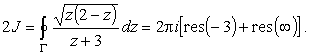
|
(28) |
Откуда
J = ip [
res(-3) + res( Ґ )].
Перейдем к вычислению вычетов:
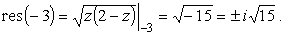
|
(29) |
Чтобы решить, какому из этих двух значений равен вычет выбранной
ветви функции, необходимо осуществить аналитическое продолжение
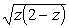 с верхнего берега разреза, где
с верхнего берега разреза, где
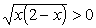 ,
в точку z = -3 (аналогичная процедура проводилась в примере 10
части 1). Для этого представим
z = r1
eij1
и
z - 2 = r2
eij2
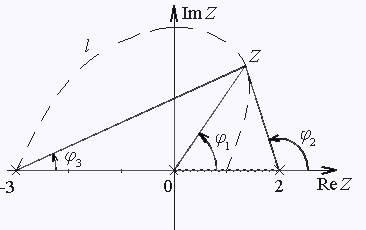
(углы
j1
и
j2
для некоторого произвольного z показаны на рис.7).
Тогда
,
в точку z = -3 (аналогичная процедура проводилась в примере 10
части 1). Для этого представим
z = r1
eij1
и
z - 2 = r2
eij2
(углы
j1
и
j2
для некоторого произвольного z показаны на рис.7).
Тогда
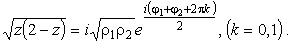
|
(30) |
На верхнем берегу разреза
j1 = 0,
j2 = p
и
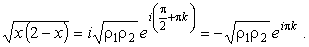
|
(31) |
|
Чтобы это выражение было положительной величиной, необходимо
выбрать k = 1. Таким образом, ветвь
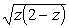 ,
которая была выбрана для интегрирования, определяется равенством ,
которая была выбрана для интегрирования, определяется равенством
|
|
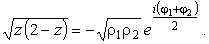
|
(32) |
|
Осуществим переход с верхнего берега разреза в точку z = -3
по произвольному пути l, не пересекающему линии разреза.
Например, выберем путь l, показанный на рис.7. Тогда в точке
z = -3 будем иметь
j1 =
p,
r1 = 3
и
j2 =
p,
r2 = 5,
и значит
|
| Рис 7. |
|
|
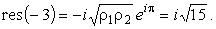
|
(33) |
для определения
res ( Ґ )
разложим функцию в ряд Лорана в окрестности бесконечно удаленной
точки
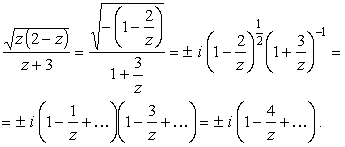
|
(34) |
Чтобы решить, какое разложение отвечает выбранной ветви функции,
осуществим аналитическое продолжение
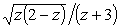 с верхнего берега в бесконечность. С учетом (32) имеем
с верхнего берега в бесконечность. С учетом (32) имеем
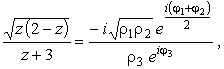
|
(35) |
где
r3
eij3 =
z + 3.
Устремим z в бесконечность, например, вверх по мнимой оси.
Тогда при
z ® Ґ
имеем
r1 =
r2 =
r3
и
j1 =
j2 =
j3 =
p/2
и (35) дает
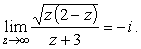
|
(36) |
Таким образом, ряд Лорана для выбранной ветви функции в
окрестности бесконечно удаленной точки следующий вид:
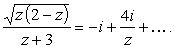
|
(37) |
Откуда
res ( Ґ ) = -4i.
Окончательно
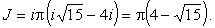
|
(38) |
дальше
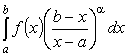 ,
где f (x) - рациональная функция, а
a
не является целым числом. Подынтегральная функция имеет
точки ветвления при
z = a и z = b , в то время как бесконечно удаленная
точка не будет точкой ветвления. Таким образом, для выделения
однозначной аналитической ветви функции достаточно сделать разрез,
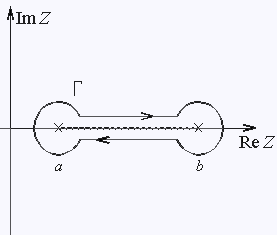
соединяющий точки a и b. Сделаем этот разрез по прямой и
рассмотрим интеграл по замкнутому контуру Г, показанному на рис.6.
,
где f (x) - рациональная функция, а
a
не является целым числом. Подынтегральная функция имеет
точки ветвления при
z = a и z = b , в то время как бесконечно удаленная
точка не будет точкой ветвления. Таким образом, для выделения
однозначной аналитической ветви функции достаточно сделать разрез,
соединяющий точки a и b. Сделаем этот разрез по прямой и
рассмотрим интеграл по замкнутому контуру Г, показанному на рис.6.
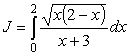 .
Здесь точки вставления при z = 0 и z = 2.
Соединим их разрезом и выберем, например, ту ветвь функции,
которая на верхнем берегу разреза принимает положительные
значения. Очевидно, на нижнем берегу разреза подынтегральная
функция будет отличаться лишь знаком. Поэтому интегралы по
верхнему и нижнему берегам в сумме дадут 2J. Интегралы по
окружностям
.
Здесь точки вставления при z = 0 и z = 2.
Соединим их разрезом и выберем, например, ту ветвь функции,
которая на верхнем берегу разреза принимает положительные
значения. Очевидно, на нижнем берегу разреза подынтегральная
функция будет отличаться лишь знаком. Поэтому интегралы по
верхнему и нижнему берегам в сумме дадут 2J. Интегралы по
окружностям
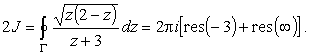
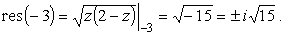
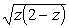 с верхнего берега разреза, где
с верхнего берега разреза, где
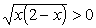 ,
в точку z = -3 (аналогичная процедура проводилась в примере 10
части 1). Для этого представим
,
в точку z = -3 (аналогичная процедура проводилась в примере 10
части 1). Для этого представим
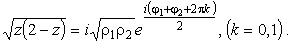
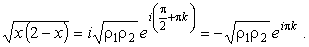

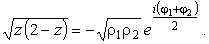
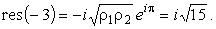
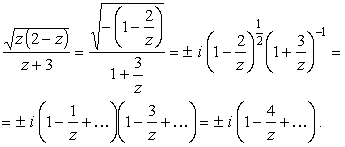
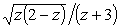 с верхнего берега в бесконечность. С учетом (32) имеем
с верхнего берега в бесконечность. С учетом (32) имеем