2.5. Интегралы вида
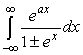
Интегралы, содержащие показательную функцию в числителе и знаменателе подынтегральной функции, часто не попадают под действие леммы Жордана. Выбор пути, замыкающего контур интегрирования тогда можно попытаться осуществить подобно тому, как это сделано в следующем примере.
В электронной теории металлов возникает необходимость вычисления
интеграла
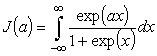 ,
где
,
где
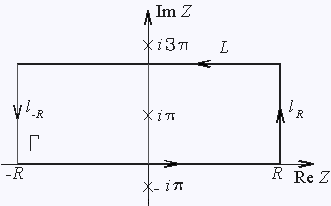
|
Здесь нельзя воспользоваться методами пунктов 2.2
и 2.3,
так как условия леммы 1 и 2
не выполнены ни в верхней, ни в
нижней полуплоскости. Попытаемся подобрать путь, замыкающий
контур интегрирования так, чтобы интеграл по нему выражался
через искомый. А именно, выберем контур интегрирования в виде
границы прямоугольника (рис. 8). Интеграл по прямой L
|
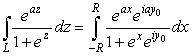
|
(49) |
| Рис 8. |
будет выражаться через искомый интеграл, если выбрать
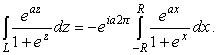
|
(50) |
Тогда контурный интеграл
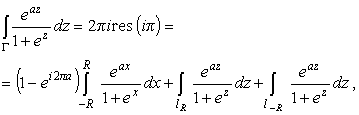
|
(51) |
где через lR и l-R обозначены пути
интегрирования по отрезкам
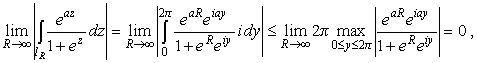 (a < 1)
(a < 1)
|
(52) |
И аналогично для l-R при a > 0.
После предельного перехода
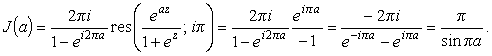
|
(53) |
Результат (53) можно получить другим способом. Для этого рассмотрим
значение интеграла
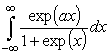 с комплексным
с комплексным
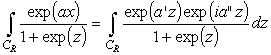 ,
если последовательность дуг CR , лежащих в верхней полуплоскости,
выбрать так, чтобы дуги не проходили через особые точки
,
если последовательность дуг CR , лежащих в верхней полуплоскости,
выбрать так, чтобы дуги не проходили через особые точки
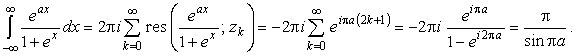
|
(54) |
В (54) для суммирования ряда мы воспользовались формулой суммы бесконечной геометрической прогрессии. Результат (54), полученный для комплексных a с Ima>0, далее аналитически продолжается на действительные значения a, что и приводит к соотношению (53).