Дополнительная сложность, возникающая при вычислении определенных
интегралов с помощью контурного интегрирования, состоит в том,
что во многих случаях приходится интегрировать по контуру со всем
не ту функцию, от которой вычисляется определенный интеграл.
Наиболее широко используется прием, в котором подынтегральная
функция домножается на логарифм. Идея этого метода содержится в
п.3.4 и состоит в следующем. Если рассмотреть контурный интеграл
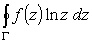 ,
где контур Г имеет вид, изображенный на рис.8 (аналогично рис.3.),
то интегралы по верхнему и нижнему берегам разреза в сумме дадут
,
где контур Г имеет вид, изображенный на рис.8 (аналогично рис.3.),
то интегралы по верхнему и нижнему берегам разреза в сумме дадут
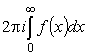 ,
так как члены с логарифмом сокращаются (см. формулу (18)).
Таким образом, контурный интеграл
,
так как члены с логарифмом сокращаются (см. формулу (18)).
Таким образом, контурный интеграл
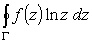 можно использовать для вычисления интеграла
можно использовать для вычисления интеграла
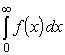 .
При этом для функции f (x) не требуется четность или
выполнение условий п.3.1.
.
При этом для функции f (x) не требуется четность или
выполнение условий п.3.1.
|
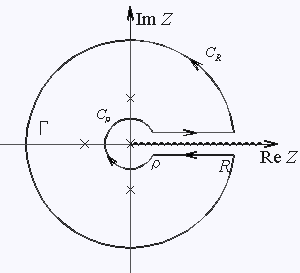
Вычислим
|
||
|
Домножим подынтегральную функцию на Ln z, получившаяся функция
|
|
| Рис 8. | ||
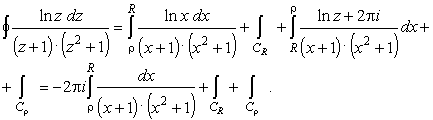
|
(39) |
В пределе
R ® Ґ
и
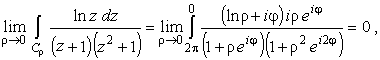
|
(40) |
так как промежуток интегрирования конечен, а
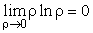 .
С другой стороны, контурный интеграл в (39) может быть найден
по основной теореме теории вычетов.
Подынтегральная функция внутри
контура интегрирования имеет три простых полюса в точках
.
С другой стороны, контурный интеграл в (39) может быть найден
по основной теореме теории вычетов.
Подынтегральная функция внутри
контура интегрирования имеет три простых полюса в точках
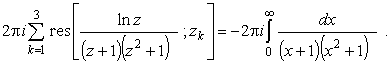
|
(41) |
Откуда
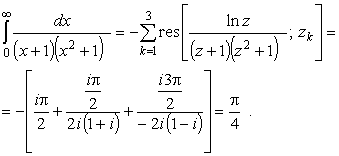
|
(42) |
Аналогичный метод можно применить и при вычислении интегралов в
конечных пределах от рациональных функций
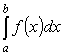 .
Для этого рассмотрим интеграл
.
Для этого рассмотрим интеграл
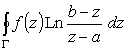 по контуру, показанному на рис.9.
по контуру, показанному на рис.9.
|
Вычислим
|
||
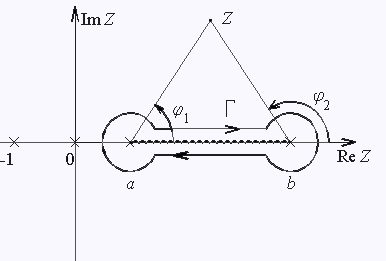
|
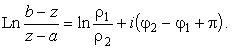
|
(43) |
|
Тогда на верхнем берегу разреза, где
|
||
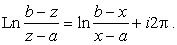
|
(44) | |
| Рис 9. | ||
А на нижнем, где, например,
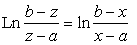
|
(45) |
Поэтому
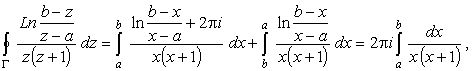
|
(46) |
так как интегралы по окружностям стремятся к нулю. Тогда
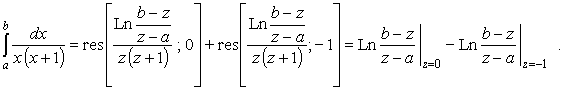
|
(47) |
Используя (43) и аналитически продолжая
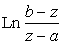 в точки 0 и -1, получим
в точки 0 и -1, получим
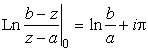 и
и
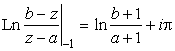 .
Откуда
.
Откуда
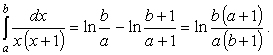
|
(48) |
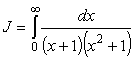 .
.
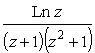
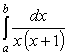 ,
0 < a < b. Рассмотрим контурный интеграл
,
0 < a < b. Рассмотрим контурный интеграл
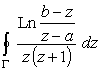 (см. рис.9). Представим
(см. рис.9). Представим