2.2. Интегралы в бесконечных пределах от рациональных функций
В п. 2.1 мы свели определенный интеграл к
контурному с помощью замены.
Чаще, однако, находят действительный определенный интеграл
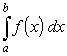 ,
рассматривая его как часть комплексного контурного интеграла
,
рассматривая его как часть комплексного контурного интеграла
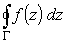 ,
вычисляемого по основной теореме теории вычетов, при условии,
что Г включает в себя интервал (а ,b) действительной оси.
При этом, конечно, возникает вопрос, какой вклад в интеграл
вносит остальная часть контура Г.
,
вычисляемого по основной теореме теории вычетов, при условии,
что Г включает в себя интервал (а ,b) действительной оси.
При этом, конечно, возникает вопрос, какой вклад в интеграл
вносит остальная часть контура Г.
Рассмотрим интеграл в бесконечных пределах
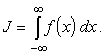
|
(7) |
|
Несобственный интеграл в бесконечных пределах понимается, как
|
|
| Рис 1. | ||
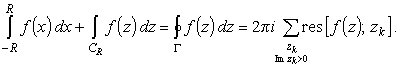
|
(8) |
Вычислит интеграл по полуокружности
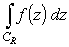 ,
вообще говоря, нисколько не проще, чем искомый интеграл
,
вообще говоря, нисколько не проще, чем искомый интеграл
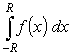 ,
но если f(z) в бесконечности стремиться к нулю столь быстро, что
,
но если f(z) в бесконечности стремиться к нулю столь быстро, что
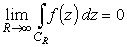 ,
то ситуация упрощается. Тогда из соотношения (8) в пределе
,
то ситуация упрощается. Тогда из соотношения (8) в пределе
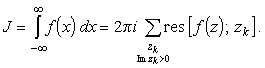
|
(9) |
В необходимых случаях путь интегрирования можно замкнуть и снизу,
т.е. другой
Вычислим интеграл
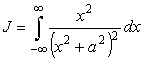 ,
встречающийся в физических расчетах. Рассмотрим
,
встречающийся в физических расчетах. Рассмотрим
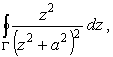
|
(10) |
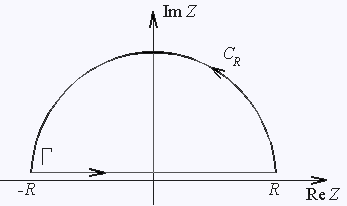
где замкнутый контурный интегрирования Г показан на рис. 1.
Из двух особых точек
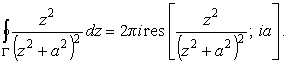
|
(11) |
С другой стороны, контур Г состоит из двух частей: отрезка
действительной оси
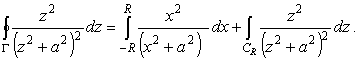
|
(12) |
Из (11) и (12) найдем
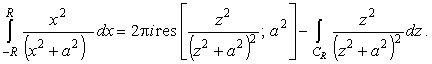
|
(13) |
Переходя в (13) к пределу
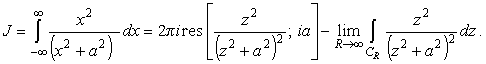
|
(14) |
Для вычисления интеграла по полуокружности представим
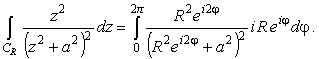
|
(15) |
Так как промежуток интегрирования в (15) конечен,
а подынтегральная функция с ростом R стремиться к нулю, то
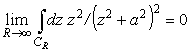 ,
и согласно (14)
,
и согласно (14)
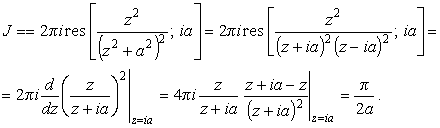
|
(16) |
Конечно, такую оценку интеграла по СR в каждом конкретном случае можно и не делать, если сформулировать в общем, виде условия, при которых интеграл по полуокружности СR стремиться к нулю. Известно, что модуль интеграла не превосходит произведения максимума модуля подынтегральной функции на длину пути интегрирования. Длина дуги СR равна pR и значит
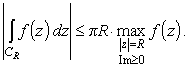
|
(17) |
Чтобы это выражение стремилось к нулю при
Пусть функция f(z) является аналитической в области
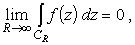
|
(18) |
где CR - полуокружность
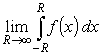 .
Пусть f(x) допускает аналитическое продолжение на комплексные
значения аргумента.
Возьмем замкнутый контур, состоящий из отрезка [-R, R]
действительной оси и полуокружности CR
.
Пусть f(x) допускает аналитическое продолжение на комплексные
значения аргумента.
Возьмем замкнутый контур, состоящий из отрезка [-R, R]
действительной оси и полуокружности CR