Интегралы вида
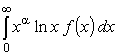 ,
содержащие как логарифмическую функцию, так и корень,
вычисляются аналогично интегралам п. 3.3,
с использованием контура
интегрирования, представленного на рис.3. Функция f (x)
должна быть рациональной, иначе трудно предположить,
что интеграл по СR удастся вычислить.
Рассмотрим это тип интегралов на примере.
,
содержащие как логарифмическую функцию, так и корень,
вычисляются аналогично интегралам п. 3.3,
с использованием контура
интегрирования, представленного на рис.3. Функция f (x)
должна быть рациональной, иначе трудно предположить,
что интеграл по СR удастся вычислить.
Рассмотрим это тип интегралов на примере.
|
Вычислим главное значение интеграла
|
||
|
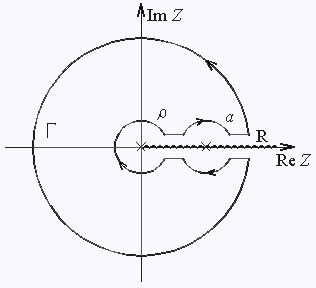
Наличие особой точки на пути интегрирования приводит к необходимости несколько модернизировать контур интегрирования по сравнению с рис.3. А именно, необходимо обойти точку z = a так, как это показано на рис.5. Тогда |
|
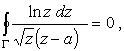 |
(23) | |
|
так как особых точек внутри Г нет. С другой стороны, после
предельных переходов
|
||
| Рис 5. | ||
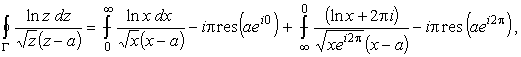
|
(24) |
где была выбрана ветвь функции, соответствующая изменению arg z
от 0 (на верхнем берегу разреза) до
2p
(нижнем берегу разреза), и учтено, что интегралы по окружностям
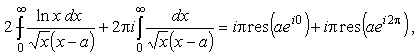
|
(25) |
для нахождения искомого интеграла достаточно взять действительную часть от (25). Тогда
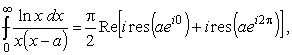
|
(26) |
поскольку член
 чисто мнимый. Если бы это было не так, то вычисления пришлось бы проводить
отдельно, например, методом п.3.3.
чисто мнимый. Если бы это было не так, то вычисления пришлось бы проводить
отдельно, например, методом п.3.3.
Из (26) имеем
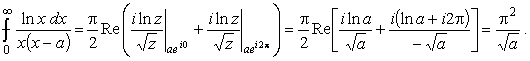
|
(27) |
Кроме разобранных в пп. 3.1- 3.5, существуют и другие типы интегралов в полубесконечных пределах, сводящиеся к контурным, но на них мы останавливаться не будем.
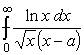 ,
(a > 0).
,
(a > 0).