К этому типу относятся интегралы вида
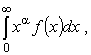
|
(11) |
где a - нецелое действительное число, f(x) - рациональная функция.Интеграл (11), рассматриваемый как функция параметра a, есть преобразование Меллина функции f(x). Это преобразование применяется в математической физике и в аналитической теории чисел.
|
Для вычисления интеграла (11) аналитически продолжим
подынтегральную функцию на комплексную плоскость. Функция
|
||
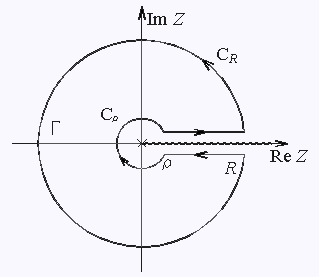
|
Пусть интегралы по дугам CR и
Cr
стремятся к нулю при
|
|
| Рис 3. | ||
Вычислим интеграл
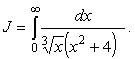 Аналитическое продолжение подынтегральной функции представляет
собой многозначную (трехзначную) функцию
Аналитическое продолжение подынтегральной функции представляет
собой многозначную (трехзначную) функцию
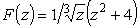 .
Разрез комплексной плоскости по действительной оси как это
показано на рис.3, разбивает данную функцию на три однозначные
ветви. Можно выбрать любую из них. Обычно используют ту ветвь
функции. Которая на верхнем берегу разреза принимает действительные
положительные значения. Если представить
.
Разрез комплексной плоскости по действительной оси как это
показано на рис.3, разбивает данную функцию на три однозначные
ветви. Можно выбрать любую из них. Обычно используют ту ветвь
функции. Которая на верхнем берегу разреза принимает действительные
положительные значения. Если представить
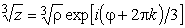 ,
то данная ветвь получится при
,
то данная ветвь получится при
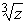 при z = x на верхнем берегу разреза равен
при z = x на верхнем берегу разреза равен
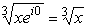 ,
а на нижнем
,
а на нижнем
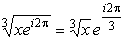 .
.
Интеграл по контуру Г, представленному на рис.3, разбивается на сумму интегралов
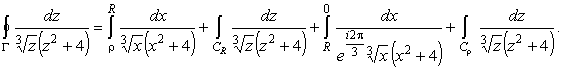
|
(12) |
С другой стороны, по основной теореме теории вычетов
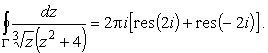
|
(13) |
Осуществим предельные переходы
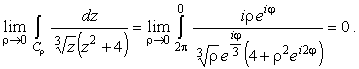
|
(14) |
Таким образом,
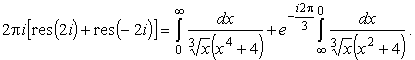
|
(15) |
Откуда
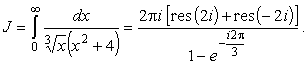
|
(16) |
Вычисление вычетов в
полюсах первого порядка
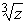 ,
соответствующие данной ветви функции. В нашем случае имеем
,
соответствующие данной ветви функции. В нашем случае имеем
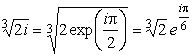 и
и
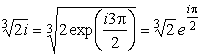 .
Поэтому
.
Поэтому
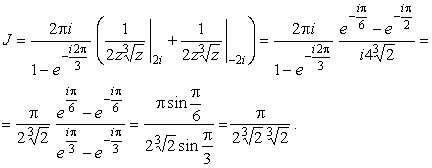
|
(17) |
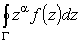 ,
который может быть вычислен с помощью теории вычетов.
,
который может быть вычислен с помощью теории вычетов.