2.4. Простой полюс на пути интегрирования
Главное значение интеграла
До сих пор предполагалось, что особые точки подынтегральной функции не лежат на пути интегрирования. Рассмотрим теперь ситуацию, когда путь интегрирования проходит через простой полюс. В этом случае, строго говоря, интегралу нельзя приписать никакого определенного значения. Однако на практике встречаются интегралы такого рода.
Для действительной переменной, когда f(x) имеет простой
полюс при x = x0, из пути интегрирования вырезают отрезок от
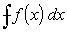
Аналогично, если путь интегрирования на комплексной плоскости проходит через простой полюс z0, то главное значение такого интеграла определится следующим образом: около точки z0 описывается маленькая окружность радиуса r, из пути интегрирования вырезается часть, попавшая внутрь этой окружности, и затем r устремляется к нулю. Интегрирование по такому пути и даст главное значение интеграла.
Чтобы сделать возможным применение теории вычетов, нужно добавить к этому разорванному пути полуокружность бесконечного малого радиуса, описанную вокруг полюса z0. Интегрирование по такой полуокружности вокруг полюса дает
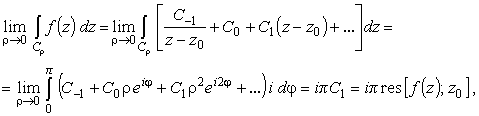
|
(34) |
если это интегрирование производится в положительном направлении по отношению к точке z0 .Из (34) видно, что вклад в интеграл в два раза меньше, чем полюса, попавшего внутрь контура. Поэтому иногда используется термин "полувычет". Таким образом, контурный интеграл, проходящий через полюс, сводится к сумме главного значения интеграла и полувычета.
Рассмотрим пример, приводящий к интегралу в смысле главного значения.
|
Вычислим интеграл
|
||
|
И теперь на пути возник простой полюс |
|
| Рис 4. | ||
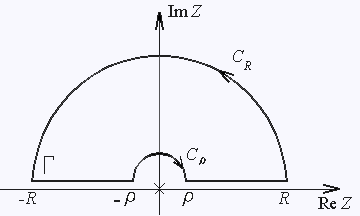
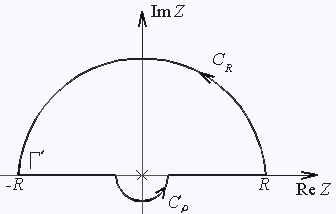
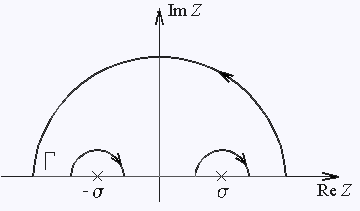
Рассмотрим контурный интеграл
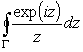 ,
где Г контур, представленный на рис. 4.
Подынтегральная функция не имеет особых точек внутри Г,
поэтому контурный интеграл равен нулю. С другой стороны,
он выражается через сумму интегралов
,
где Г контур, представленный на рис. 4.
Подынтегральная функция не имеет особых точек внутри Г,
поэтому контурный интеграл равен нулю. С другой стороны,
он выражается через сумму интегралов
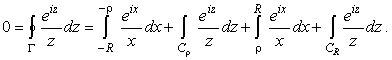
|
(35) |
После предельных переходов
R ® Ґ,
r ® 0,
интегралы по действительной оси в сумме дадут
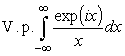 ,
интеграл по дуге
Cr
(направление обхода отрицательное) даст
,
интеграл по дуге
Cr
(направление обхода отрицательное) даст
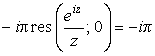 ,
а интеграл по дуге CR - нуль в силу
леммы Жордана.
Поэтому (35) сведется к равенству
,
а интеграл по дуге CR - нуль в силу
леммы Жордана.
Поэтому (35) сведется к равенству
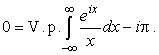
|
(36) |
Откуда
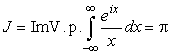 .
.
|
Полюс в точке с таким же правом можно обойти и снизу (рис. 5). |
||
|
Результат вычисление при этом не изменится.
Действительно, так как внутри контура Г' лежит полюс
|
|
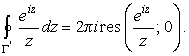
|
(37) | |
|
С другой стороны, контурный интеграл выражается через сумму интегралов |
||
| Рис 5. | ||
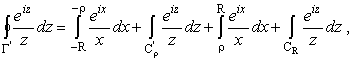
|
(38) |
где теперь дугу полуокружности
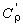 проходим в положительном направлении относительно точки
проходим в положительном направлении относительно точки
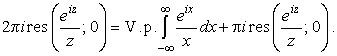
|
(39) |
Откуда по-прежнему
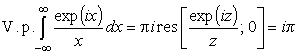 .
.
Не следует считать, что при наличии полюса на пути интегрирования всегда используется главное значение интеграла. Другой способ решения заключается в том, что полюс смещают с контура интегрирования, а затем переходят к пределу, при котором он возвращается в старое положение. Физические соображения диктуют, какой способ следует избрать в конкретном случае. Поясним это примером.
В квантовой теории рассеяния встречается функции
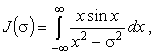
|
(40) |
|
где s - действительное и положительное. Из физических условий следует, что функция J(s) должна иметь форму eis, так как это - расходящаяся рассеянная волна. |
||
|
Вычислим главное значение интеграла (40). Для чего представим
|
|
| Рис 6. | ||
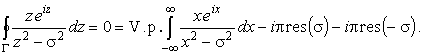
|
(41) |
Откуда
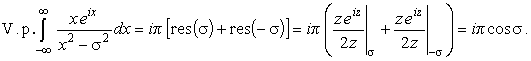
|
(42) |
Окончательно
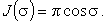
|
(43) |
В математическом смысле мы получили точное выражение для интеграла (40), однако косинусоидальная зависимость соответствует стоячей волне, тогда как нам необходимо выделить в решении расходящуюся рассеянную волну. Попытаемся получить решение требуемой формы, которое удовлетворяло бы физическим условиям задачи. Вместо обхода особых точек сместим их с вещественной оси, заменив s® s + ie, где положительный параметр e мал по величине и в конечном результате полагается равным нулю, т.е.
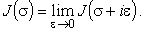
|
(44) |
Тогда особые точки подынтегральной функции
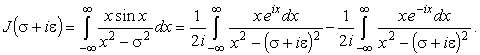
|
(45) |
|
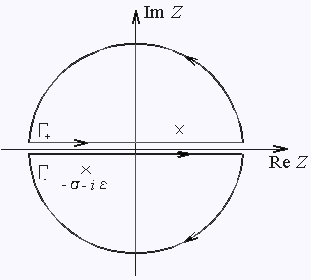
Для вычисления первого интеграла в (45) замкнем путь интегрирования полуокружностью бесконечного радиуса в верхней полуплоскости, а для вычисления второго - в нижней (контуры интегрирования Г+ и Г- на рис. 7). Тогда для первого интеграла находим |
||
|
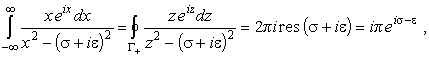
|
(46) |
|
а для второго |
||
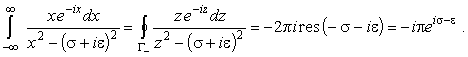
|
(47) | |
| Рис 7. | ||
Отсюда
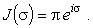
|
(48) |
Этот результат соответствует граничным условиям задачи о рассеянии.
Отметим, что подстановка
Часто правило обхода полюсов связывается с получением физически реального затухающего решения. Так и в этом примере можно трактовать is как мнимую добавку к волновому вектору, описывающую (при s > 0 ) затухающие волны. Впервые правило обхода полюсов ( s® s + ie ) было установлено Л.Д. Ландау в 1946 г.
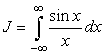 .
Подынтегральная функция не имеет особенностей на пути интегрирования,
но в соответствии с методом п.
.
Подынтегральная функция не имеет особенностей на пути интегрирования,
но в соответствии с методом п. 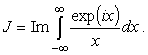
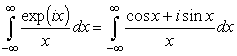 не является сходящимся. Но это относится к его действительной части
не является сходящимся. Но это относится к его действительной части
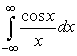 ,
тогда как мнимая часть конечна. Для ее вычисления и можно
воспользоваться, например,
,
тогда как мнимая часть конечна. Для ее вычисления и можно
воспользоваться, например, 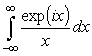 .
.
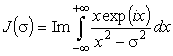 и рассмотрим этот интеграл в комплексной плоскости.
Дополним путь интегрирования полуокружностью бесконечного радиуса
в верхней полуплоскости (при
и рассмотрим этот интеграл в комплексной плоскости.
Дополним путь интегрирования полуокружностью бесконечного радиуса
в верхней полуплоскости (при