При вычислении определенных интегралов мы до сих пор стремились замкнуть путь интегрирования таким образом, чтобы возникший дополнительный интеграл стремился к нулю или выражался через искомый интеграл. Существует еще одна возможность - выбрать путь, замыкающий контур интегрирования, таким образом, чтобы интеграл по нему известен. Рассмотрим этот метод на примере.
Вычислим важные в теории дифракции интегралы Френеля
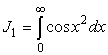 и
и
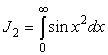 .
.
|
Задача фактически сводится к вычислению одного комплексного
интеграла
|
||
|
Для того чтобы iz2 перешло в
-r2,
должно быть
|
|
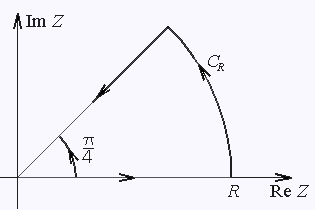
| Рис 2. | ||
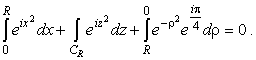
|
(8) |
Трудности возникают лишь с оценкой интеграла по CR. Именно
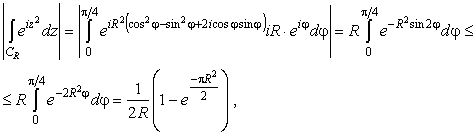
|
(9) |
где подставлено
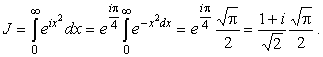
|
(10) |
Окончательно
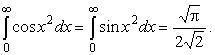
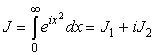 .
Наиболее близок к искомому интеграл Пуассона
.
Наиболее близок к искомому интеграл Пуассона
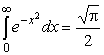 .
В связи с этим попробуем выбрать путь, замыкающий контур
интегрирования так, чтобы интеграл по нему выражался через
интеграл Пуассона.
.
В связи с этим попробуем выбрать путь, замыкающий контур
интегрирования так, чтобы интеграл по нему выражался через
интеграл Пуассона.
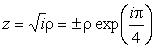 .
.