Рассмотрим интеграл
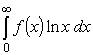 ,
где f(x) - рациональная функция. Естественно, в качестве
f(x) можно брать только такие функции, при которых интеграл является
сходящимся.
,
где f(x) - рациональная функция. Естественно, в качестве
f(x) можно брать только такие функции, при которых интеграл является
сходящимся.
Подынтегральная функция, аналитически продолженная на комплексную
плоскость, имеет точки ветвления логарифмического типа при
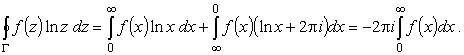
|
(18) |
|
Видно, что искомый интеграл
|
||
|
В случае, если функция f(x) четная, т.е. выполняется соотношение f(-x) = f(x) , вычисление данного интеграла можно осуществить следующим путем. |
|
|
Рассмотрим контурный интеграл
|
||
| Рис 4. | ||
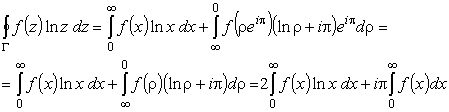
|
(19) |
где была использована четность f (x). Отсюда
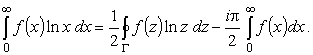
|
(20) |
Контурный интеграл вычисляется по основной теореме, а интеграл
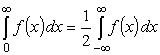 относится к виду, разобранному в п. 2.2 и требует отдельного
вычисления. Если воспользоваться результатом п.2.2
(формула (9) часть 2), то
относится к виду, разобранному в п. 2.2 и требует отдельного
вычисления. Если воспользоваться результатом п.2.2
(формула (9) часть 2), то
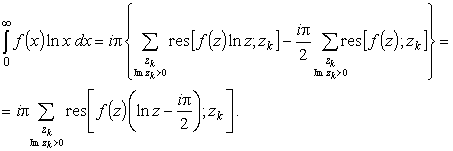
|
(21) |
Прежде чем использовать подобного рода формулы для вычисления конкретного интеграла, необходимо тщательно проверить выполнение всех условий, наложенных на f(x) . Еще лучше повторить вычисления, приводящие к такой формуле с конкретной функцией, так как иногда некоторые условия, накладываемые на f (x), в явном виде не формируются. Так, например, при выводе (21) неявно предполагалось, что f (x) не имеет особых точек на действительной оси.
Коротко разберем случай, когда f (x) не является четной.
Здесь для вычисления
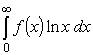 следует рассмотреть интеграл
следует рассмотреть интеграл
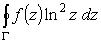 по контуру Г, указанному на рис.3. Интегралы по верхнему и
нижнему берегам разреза тогда дадут
по контуру Г, указанному на рис.3. Интегралы по верхнему и
нижнему берегам разреза тогда дадут
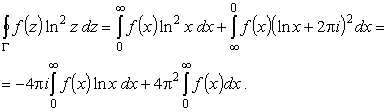
|
(22) |
Из последней формулы можно найти искомый интеграл, если
предварительно вычислить
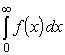 .
Такой же прием применяют и при вычислении интегралов,
содержащих lnm x.
.
Такой же прием применяют и при вычислении интегралов,
содержащих lnm x.
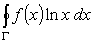 .
Контур Г изображен на рис.4, линия разреза может быть любой,
важно лишь, чтобы она лежала в нижней полуплоскости.
Выберем ту ветвь Ln z, для которой при
.
Контур Г изображен на рис.4, линия разреза может быть любой,
важно лишь, чтобы она лежала в нижней полуплоскости.
Выберем ту ветвь Ln z, для которой при