2.3. Интегралы от осциллирующих функций в бесконечных пределах
Рассмотрим вычисление несобственных интегралов вида
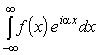
|
(19) |
и интегралов
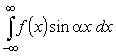 ,
,
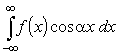 ,
очевидным образом сводящихся к (19). При этом будем предполагать,
что f(z) рациональная функция. Интегралы такого рода возникают при
разложении функций в ряды и интеграл Фурье и играют важную роль
во многих физических задачах.
,
очевидным образом сводящихся к (19). При этом будем предполагать,
что f(z) рациональная функция. Интегралы такого рода возникают при
разложении функций в ряды и интеграл Фурье и играют важную роль
во многих физических задачах.
Особенность вычисления этих интегралов по сравнению с интегралами
от рациональных функций (п. 2.2) обусловлена тем, что
лемма 1,
вообще говоря, не применима к функции
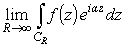 ,
поясняющее содержание данной леммы. А именно, положив
,
поясняющее содержание данной леммы. А именно, положив
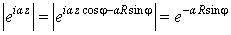 .
Эта величина при
.
Эта величина при
Пусть функция f(z) является аналитической в области
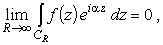
|
(20) |
где CR - полуокружность
При
Лемма Жордана остается справедливой и в том случае,
когда функция f(z) удовлетворяет сформулированным выше условиям
в полуплоскости
Вычислим интеграл
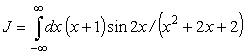 .
Поскольку лемма 2 не применима к интегралу
.
Поскольку лемма 2 не применима к интегралу
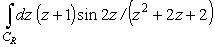 ни в нижней, ни в верхней полуплоскости, представим
ни в нижней, ни в верхней полуплоскости, представим
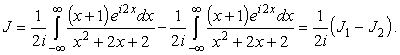
|
(21) |
|
При вычислении интегралов J1 и J2 уже можно воспользоваться леммой Жордана. А именно |
|
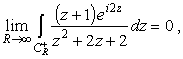 |
(22) | |
|
для дуги
|
||
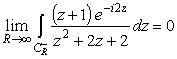 |
(23) | |
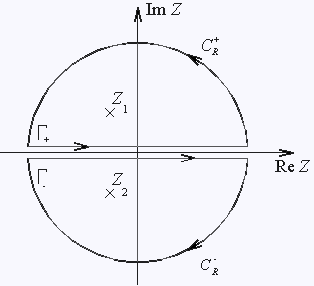
| Рис 2. | ||
для дуги
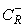 ,
лежащей в нижней полуплоскости.
Поэтому рассмотрим следующие контурные интегралы (см. рис. 2):
,
лежащей в нижней полуплоскости.
Поэтому рассмотрим следующие контурные интегралы (см. рис. 2):
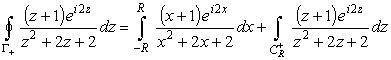
|
(24) |
и
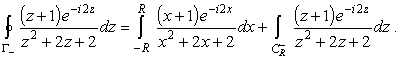
|
(25) |
В пределе
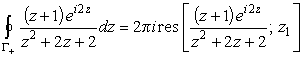
|
(26) |
и
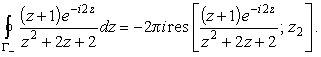
|
(27) |
Знак минус в (27) обусловлен отрицательной ориентацией контура Г- относительно особой точки z2. Тогда из (21), с учетом (24) - (27), получим
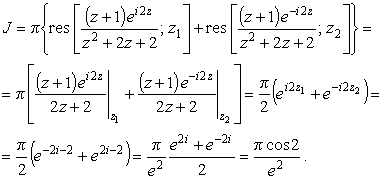
|
(28) |
В подобных примерах нет необходимости вычислять два интеграла
J1 и J2, достаточно вычислить один из них,
например J1, если поступить следующем образом. В интеграле
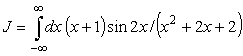 представим
представим
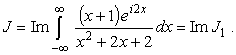
|
(29) |
Найдем J1, вычислив контурный интеграл (26). Имеем
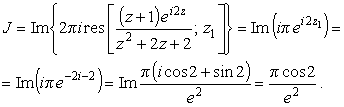
|
(30) |
Кроме приложения к рядам Фурье, интегралы, сходные с (19), встречаются в формуле обращения преобразования Лапласа. Интегральное преобразование Лапласа или операционное исчисление широко используется для решения различных физико-технических задач, сводящихся к линейным дифференциальным уравнениям в частных или полных производных. Формула обращения выглядит так:

|
(31) |
где с помощью пределов
Замена
Вычислим интеграл
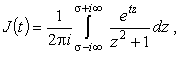 , где s > 0.
, где s > 0.
|
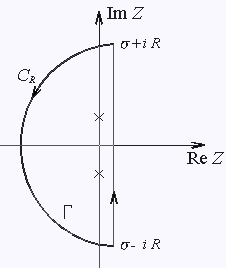
|
Рассмотрим интеграл по прямой
|
|
| Рис 3. | ||
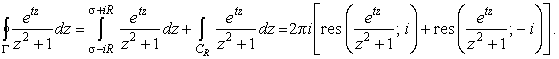
|
(32) |
В пределе R ® Ґ, отсюда получим
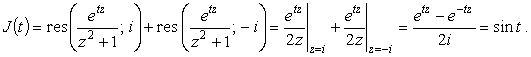
|
(33) |
Для t<0 лемма Жордана выполняется в правой полуплоскости.
Путь интегрирования от
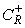 ,
лежащей в верхней полуплоскости (т.к.
,
лежащей в верхней полуплоскости (т.к.
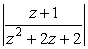 ~
~
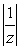 при
при