1.5. Многозначные аналитические функции
Если одному и тому же значению z отвечает не одно, а несколько
(или даже счетное множество) значений F(z), то такая функция называется
многозначной.
Многозначными являются функции
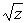 ,
,
Точка
Если с помощью разрезов плоскости комплексной переменной исключить возможность обхода точек ветвления, то многозначная функция F(z) распадается на несколько однозначных ветвей fk(z). Для каждой однозначной аналитической ветви fk(z) основная теорема теории вычетов справедлива в области, не содержащей разрезы. Задание конкретной ветви многозначной аналитической функции осуществляется указанием сделанных разрезов и указанием значения функции в какой-либо одной точке.
|
Найдем вычет
|
||
|
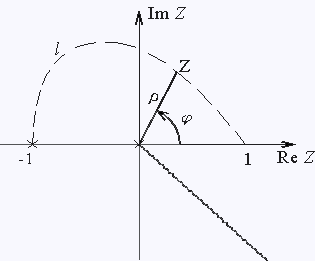
Данная функция двузначная. Вычет в простом полюсе также может иметь два значения. Согласно (8) имеем |
|
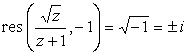 |
(31) | |
| Рис 2. | ||
Чтобы решить, какому из этих значений равен вычет указанной ветви функции,
необходимо осуществить аналитическое продолжение
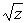 из точки
из точки 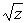 в точке
в точке
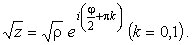
|
(32) |
Для того чтобы
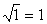 ,
надо положить k = 0, тогда при
,
надо положить k = 0, тогда при
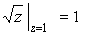 .
При движении z по кривой l угол
.
При движении z по кривой l угол
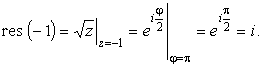
|
(33) |
Если бы разрез был проведен в верхней полуплоскости,
то аналогичное рассмотрение привело бы к значению
|
Найдем вычет
|
||
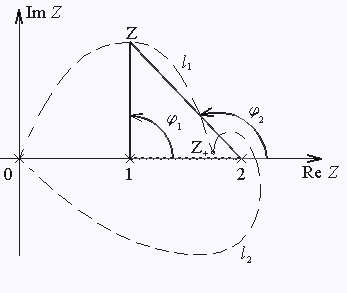
|
Слова "на верхнем берегу разреза" означают, что рассматриваются точки,
расположенные в непосредственной близости к линии разреза со стороны
верхней полуплоскости, т.е. такие, для которых |
|
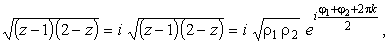 |
(34) | |
| Рис 3. | ||
где k = 0, 1. В произвольной точке z+ на верхнем берегу
разреза
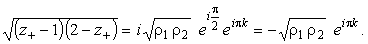
|
(35) |
Чтобы это выражение было положительной величиной, необходимо выбрать k = 1. Тогда для данной ветви функции
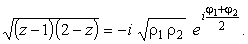
|
(36) |
Из точки z+ в точку z = 0 можно перейти по кривой
l1.
В точке z = 0 будем иметь
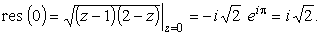
|
(37) |
Переход из z+ в z = 0 можно осуществить также по пути
l2,
тогда в точке z = 0,
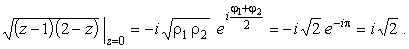
|
(38) |
Таким образом, при вычислении вычетов от многозначных функций следует обращать особое внимание на правильность выбора ветви функции.
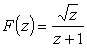 в точке
в точке 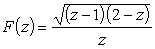 в точке z = 0 для той ветви функции,
которая на верхнем берегу разреза принимает положительные
значения (разрез показан на рис. 3).
в точке z = 0 для той ветви функции,
которая на верхнем берегу разреза принимает положительные
значения (разрез показан на рис. 3).
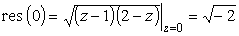 .
Но
.
Но
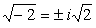 ,
и надо выяснить, какой знак здесь следует взять.
,
и надо выяснить, какой знак здесь следует взять.