Контрольные воросы
- В окрестности, каких точек аналитическая функция может быть разложена в ряд Лорана?
А в ряд Тейлора?
- В окрестности, каких особых точек нельзя разложить в ряд Лорана? Почему?
- Что называется полюсом первого порядка?
- Как выглядит разложение в ряд Лорана в окрестности полюса порядка n?
А в окрестности существенно особой точки?
- Чему равен
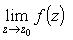 ,
если точка z0 - простой полюс, полюс порядка n, правильная точка,
существенно особая точка, точка ветвления?
,
если точка z0 - простой полюс, полюс порядка n, правильная точка,
существенно особая точка, точка ветвления?
- Что называется вычетом?
- Как определяется вычет через коэффициенты ряда Лорана?
- Чему равен вычет в правильной точке?
- Может ли вычет быть равным нулю в особой точке?
- Напишите формулы для нахождения вычета в простом полюсе и в полюсе порядка n.
- Сформулируйте основную теорему теории вычетов.
- Применима ли основная теорема к многозначным аналитическим функциям?
- Как выделить однозначную ветвь многозначной аналитической функции?
Как определяется вычет в бесконечно удаленной точке?
- В каких случаях вычет в бесконечно удаленной точке будет равен нулю?
В каких случаях он может быть отличен от нуля?
- Чему равна сумма вычетов функции во всех особых точках?
Когда это утверждение справедливо?
- Приведите пример функции, имеющей полюс первого порядка, полюс третьего порядка,
существенно особую точку. Подтвердите это разложением функции в ряд Лорана.
- Приведите пример многозначной функции. Укажите точки ветвления и их порядок.
дальше
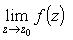 ,
если точка z0 - простой полюс, полюс порядка n, правильная точка,
существенно особая точка, точка ветвления?
,
если точка z0 - простой полюс, полюс порядка n, правильная точка,
существенно особая точка, точка ветвления?