При изучении теории вычетов наибольшие затруднения студенты испытывают в определении характера особой точки, правильном применении формулы для вычисления вычета. Особое внимание в методических указаниях уделено особенностям нахождения вычетов многозначных аналитических функций и вычетов в бесконечно удаленной точке, так как эти вопросы недостаточно полно изложены в учебниках. Для удобства основные результаты теории вычетов собраны в таблицу.

Вычетом аналитической функции f (z) в изолированной особой точке называется комплексное число

(1)

где Г - произвольный замкнутый контур, охватывающий z₀ и не содержащий других особых точек функции f(z). Интегрирование производится в положительном направлении, т.е. так, чтобы при обходе по Г точка z₀ оставалась слева (для конечных z₀ это направление против часовой стрелки).

Однозначная аналитическая функция в окрестности изолированной особой точки может быть единственным образом разложена в ряд Лорана

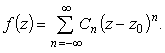
(2)

Проинтегрировав (2) по контуру Г, получим слева выражение для вычета, а справа сумму членов вида 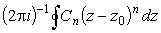, интегрирование в которых можно выполнить, сделав замену z - z₀ = r e ^ij и выбрав контур Г в виде окружности | z - z₀ | = r. Для n № -1

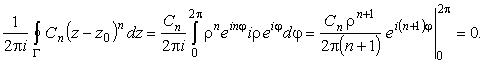
(3)

Однако для n = -1

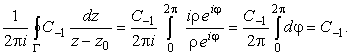
(4)

таким образом,

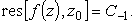
(5)

Постоянная C_-1, которая служит коэффициентом в разложении Лорана при члене ( z - z₀ )^-1, и является вычетом функции в точке z₀.

дальше