Соотношение (5) позволяет находить вычет из разложения функции в ряд Лорана в окрестности особой точки. Но задача нахождения вычета проще задачи разложения функции в ряд Лорана, так как при этом требуется только один коэффициент ряда. Оказывается, что в большинстве случаев вычисление вычета сводится к нахождению производной от некоторого выражения, содержащего f(z). Тем самым интегрирование аналитической функции по замкнутому контуру заменяется на дифференцирование этой функции. Вид формулы, используемой для вычисления вычета, зависит от того, с какого члена начинается разложение функции в ряд Лорана.

Пусть в разложении f (z) в окрестности z₀ главная часть ряда Лорана отсутствует, т.е.

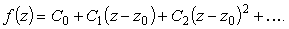
(6)

Такая точка z₀ называется устранимой особой точкой (или правильной, обыкновенной точкой функции f (z)). В окрестности такой точки f (z) ограничена, а и конечен. Очевидно, что C_-1 = 0 и, следовательно, res [ f (z), z₀ ] = 0.

Точка z₀ называется простым полюсом, или полюсом первого порядка, если в окрестности c разложение f(z) в ряд Лорана имеет вид ( C_-1 № 0 ):

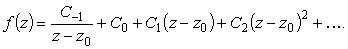
(7)

Умножим обе части этого равенства на z - z₀ и перейдем к пределу при z ® z₀. Получим формулу для вычисления вычета в простом полюсе:

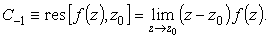
(8)

Если f(z) есть частное двух аналитических функций j ( z ) и y ( z ), т.е. f ( z ) = j ( z ) / y ( z ), причем j ( z₀ ) № 0, а y ( z ) имеет в z₀ нуль первой кратности, то из (8) с помощью правила Лопиталя нетрудно получить

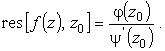
(9)

Отметим, что в полюсе первого порядка вычет обязательно отличен от нуля, а

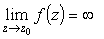
Если разложение в ряд Лорана в окрестности точки z₀ имеет вид ( C_{- n} № 0)

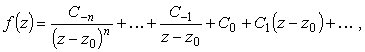
(10)

то точка z₀ называется полюсом порядка n. Умножим обе части равенства на (z - z₀)ⁿ. Это даст

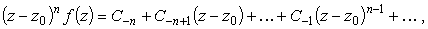
(11)

что представляет собой ряд Тейлора для функции (z - z₀)ⁿ f ( z ). Для C_-1, коэффициента перед (z - z₀)^n-1 в таком ряде Тейлора, имеем

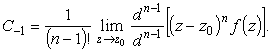
(12)

Эта формула и используется для нахождения вычета в полюсе n - го порядка. Отметим, что согласно (10) 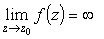. В полюсе порядка n ( n № 1) коэффициент C_-1 не обязан быть отличным от нуля, так что возможен случай, когда res [ f (z), z₀ ] = 0.

Если ряд Лорана содержит бесконечное число членов с отрицательными степенями, то точка z₀ называется существенно особой. Одно из фундаментальных различий между полюсом и существенно особой точкой заключается в том, что полюс порядка n можно устранить, умножив функцию на 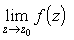(z - z₀)ⁿ. Для существования особой точки этого сделать нельзя. Отсюда, в частности, следует, что не существует. Вычет в существенно особой точке приходится находить из разложения функции в ряд Лорана.

Найдем вычеты функции f (z) = (z² - 3z + 2)^-1. Эта функция является аналитической на всей комплексной плоскости, за исключением тех точек, в которых знаменатель обращается в нуль. Квадратное уравнение z² - 3z + 2 = 0 имеет два корня z₁ = 1, z₂ = 2, оба первой кратности, и, значит, функция f(z) простые полюсы в точках z₁ и z₂. Для вычисления вычетов удобно представить z² - 3z + 2 = (z - 1)(z - 2), тогда по формуле (8)

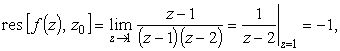
(13)

а

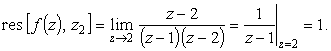
(14)

Можно было воспользоваться и формулой (9). А именно

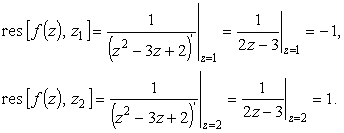
(15)

Найдем вычет f ( z ) = z^-3 e ^az в точке z = 0. Точка z = 0 является полюсом третьего порядка, и вычисление вычета нужно производить по формуле (12) с n = 3

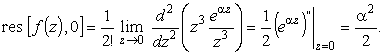
(16)

Найдем вычет f (z) = z^-6 sin z в точке z = 0. Эта точка является полюсом пятого порядка (а не шестого!), поэтому

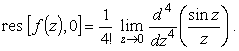
(17)

Вычисления производной и тем более предела в этом примере достаточно сложны. Вычет быстрее и проще найти из разложения функции в ряд Лорана. Воспользовавшись известным разложением синуса, получим

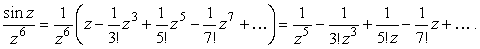
(18)

Здесь коэффициент C_-1 = 1/5!, т.е.

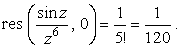
(19)

Разложение (18) подтверждает, что точка z = 0 является полюсом пятого порядка

Найдем вычет f(z) = (z ² + 1) e ^1/z в точке z = 0. Здесь мы имеем дело с существенно особой точкой. Вычет определяется из разложения функции в ряд. Имеем

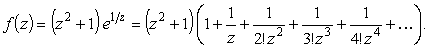
(20)

Теперь надо почленно перемножить эти выражения и найти коэффициент C_-1

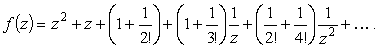
(21)

Вычет .

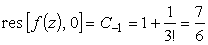дальше