1.4. Основная теорема теории вычетов
Обобщением соотношения (1) является основная теорема теории вычетов. Она утверждает, что для аналитической функции f(z), имеющей внутри замкнутого контура Г конечное число особых точек однозначного характера,
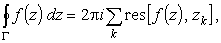
|
(26) |
где сумма берется по всем особым точкам zk, содержащимся внутри Г, а направление интегрирования предполагается положительным.
Эта теорема сводит задачу о вычислении интеграла по замкнутому контуру к нахождению вычетов в особых точках.
|
Вычислим
|
||
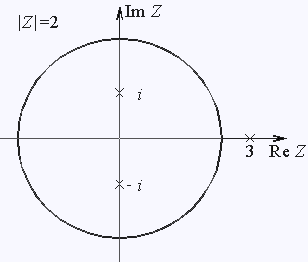
|
Из них внутрь контура интегрирования попали лишь два |
|
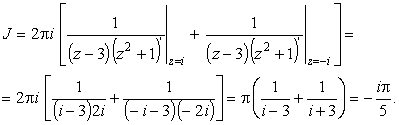 |
(27) | |
Рассмотрим f(z) из данного примера на расширенной комплексной плоскости.
Окружность
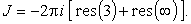
|
(28) |
При
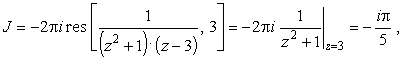
|
(29) |
что согласуется с (27).
Обобщением этого результата является следующая теорема
Если функция f(z) однозначна и аналитична во всей комплексной плоскости, за исключением только конечного числа особых точек, то сумма всех ее вычетов (включая вычет в бесконечно удаленной точке) равна нулю.
Действительно, интеграл по окружности 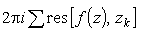 .
С другой стороны, этот интеграл выражается через
.
С другой стороны, этот интеграл выражается через
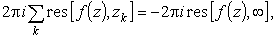
|
(30) |
из которого и следует утверждение теоремы.
Функция
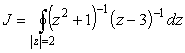 .
.