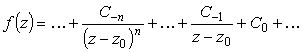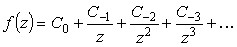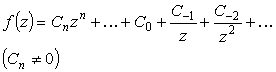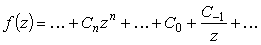Расширенная комплексная плоскость включает в себя конечные комплексные числа,
а также число
z = Ґ
Окрестностью числа
z = Ґ
будет множество точек z,
для которых справедливо соотношение | z | > R.
Вычет в бесконечно удаленной точке определяется формулой
(1),
где в качестве Г можно взять, к примеру, окружность
| z | = R.
R должно быть настолько велико, чтобы конечные столбцы точки не попали внутрь Г,
т.е. в данном случае в область
| z | > R.
Положительному направлению обхода соответствует движение по часовой стрелке.
Проинтегрировав почленно функцию, разложенную в ряд Лорана в окрестности
бесконечно удаленной точки
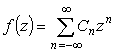
|
(22) |
так, как это делалось в (3) и
(4), получим
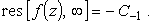
|
(23) |
Знак минус возник из-за того, что направление интегрирования по
j
теперь противоположно направлению в (4).
Формула (23) является основой для
вычисления вычета в бесконечно удаленной точке.
Классификация особенностей в бесконечно удаленной точке проводится следующим образом.
Если положить W = 1/z,
то окрестность бесконечно удаленно точки плоскости
перейдет в окрестность нуля плоскости W, и тем самым изучение поведения функции
f(z) в бесконечности сведется к изучению поведения функции в точке W = 0.
Аналогично п. 1.2
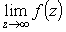 будет конечен, равен бесконечности или неопределен в зависимости от
того, будет ли точка
z = Ґ
соответственно, правильной, полюсом или существенно особой.
Но есть и важное различие. Вычет функции в бесконечно удаленной точке может быть отличен
от нуля, даже если точка
z = Ґ
является правильной для f(z). Например,
f (z) = 1/z
имеет в бесконечности правильную точку
(более того,
будет конечен, равен бесконечности или неопределен в зависимости от
того, будет ли точка
z = Ґ
соответственно, правильной, полюсом или существенно особой.
Но есть и важное различие. Вычет функции в бесконечно удаленной точке может быть отличен
от нуля, даже если точка
z = Ґ
является правильной для f(z). Например,
f (z) = 1/z
имеет в бесконечности правильную точку
(более того,
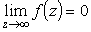 ),
но С-1 = 1 и, значит,
res ( 1/z, Ґ ) = -1.
Для удобства основные результаты теории вычетов собраны в таблицу.
В ней представлена классификация, как конечных особых точек, так и особенностей
в бесконечности и приведены формулы для вычисления вычетов.
),
но С-1 = 1 и, значит,
res ( 1/z, Ґ ) = -1.
Для удобства основные результаты теории вычетов собраны в таблицу.
В ней представлена классификация, как конечных особых точек, так и особенностей
в бесконечности и приведены формулы для вычисления вычетов.
Пример 5.
Найдем вычет
f (z) = z10 (z+1)-7
в бесконечности. При
z ® Ґ
данная функция f (z) ~ z3,
из чего можно заключить, что точка
z = Ґ
является для неё полюсом третьего порядка.
Для вычисления вычета разложим f(z) в ряд.
Считая
| z |
достаточно большим, получим:
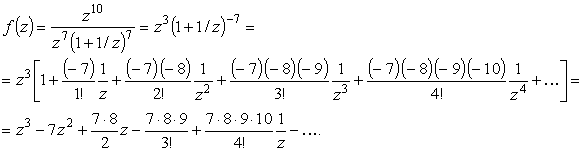
|
(24) |
Здесь был использован биноминальный ряд, что возможно для
1 / | z | < 1.
Из этого разложения видим, что
z = Ґ
действительно является полюсом третьего
порядка для f (z) и, что
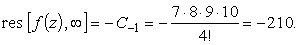
|
(25) |
Пример 6.
Найдем вычет
f ( z ) = z ( z3 + 1)-1
sin (1/ z)
в бесконечно удаленной точке.
Так как при
z ® Ґ
sin(1/z) ~ z-1, а
(z3+1)-1 ~ z-3,
то f(z) ~ z-3.
Отсюда заключаем, что точка
z = Ґ
является правильной.
Поскольку разложение данной функции в ряд Лорана начинается с члена z-3,
то C-1 и вместе с ним
res [ f ( z ),Ґ ]
равны нулю.
Пример 7.
Исследуем функцию
f ( z ) = 1/sin z
в окрестности бесконечно удаленной точки.
Данная функция имеет особые точки (полюсы первого порядка) при
z = pk,
где
k = 0, ±1, ±2,...
В любую окрестность | z | > R бесконечно удаленной точки попадает бесконечное
число этих полюсов, поэтому точка
z = Ґ
является неизолированной особой точкой.
В ней не определено понятие вычета, а также невозможно разложение в ряд Лорана
в окрестности этой точки.
Таблица 1.
Классификация особых точек и формулы для вычисления вычетов
| Тип особой точки |
Разложение функции в ряд Лорана в окрестности особой точки |
Предел
f(z)
при
z ® z0
|
Вычет |
Формула для вычисления вычета |
| z0 - правильная точка |
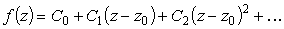
|
С0 |
0 |
- |
| z0 - простой полюс |
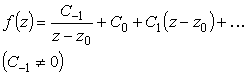
|
Ґ
|
C-1 |
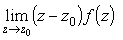 или формула (9)
или формула (9)
|
| z0 - полюс порядка n |
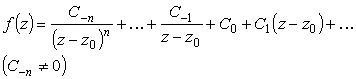
|
Ґ
|
C-1 |
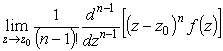 или из разложения в ряд
или из разложения в ряд
|
| z0 - существенно особая точка |
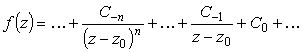
|
не существ. |
C-1 |
исключительно из разложения в ряд Лорана |
|
Ґ
- правильная точка |
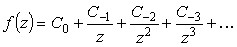
|
C0 |
-C-1 |
из разложения в ряд |
|
Ґ
- полюс порядка n |
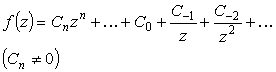
|
Ґ
|
-C-1 |
то же |
|
Ґ
-существенно особая точка |
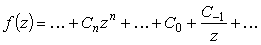
|
не существ. |
-C-1 |
- |
дальше
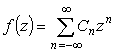
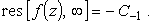
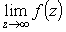 будет конечен, равен бесконечности или неопределен в зависимости от
того, будет ли точка
будет конечен, равен бесконечности или неопределен в зависимости от
того, будет ли точка
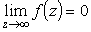 ),
но
),
но 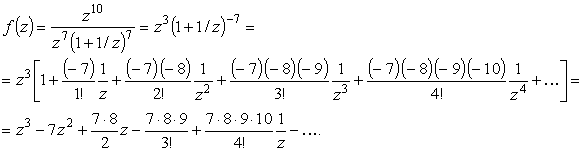
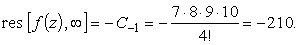
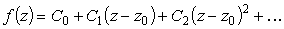
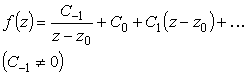
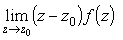 или формула (9)
или формула (9)
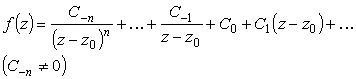
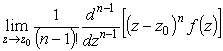 или из разложения в ряд
или из разложения в ряд