VII. ПРИМЕНЕНИЕ ЭЛЕКТРОННОЙ
СПЕКТРОСКОПИИ В ИССЛЕДОВАНИИ ПОВЕРХНОСТИ И ГРАНИЦ РАЗДЕЛА
7.1.
Количественный элементный анализ в электронной спектроскопии
Методы
электронной оже-спектроскопии и рентгеновской фотоэлектронной спектроскопии в
настоящее время наиболее широко применяются для количественного определения
атомных концентраций элементов, находящихся на поверхности. Основой
количественного анализа является тот факт, что интенсивность соответствующего
оже-пика или фотоэлектронного пика данного элемента пропорциональна
концентрации этого элемента на поверхности. Для количественного анализа в ЭОС и
РФЭС используют одни и те же подходы: вычисление интенсивности электронного
пика из первых принципов, использование эталонных образцов, учет матричных
поправок и т.д. Рассмотрим в этом разделе применение электронной оже-
спектроскопии для количественного элементного анализа.
Исходя из первых принципов,
рассматривая суммарный вклад, вносимый различными механизмами в образование
сигнала оже-электронов, можно записать в общем виде следующее выражение для
тока оже-электронов данного атома i :
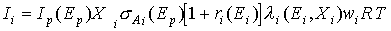 , (7.1)
, (7.1)
здесь Ip(Ep) - ток первичных
электронов с энергией Ep,
Xi - концентрация элемента i в анализируемой точке,
sAi(Ep) - сечение ионизации уровня А элемента i при энергии Ep,
[1+ri(Ei)] - фактор обратного рассеяния, характеризующий
дополнительную ионизацию уровня данного атома вторичными (рассеянными назад)
электронами,
li(Ei,Xi)
- длина свободного пробега электрона (глубина выхода),
wi - вероятность
соответствующего оже-перехода и неизлучательного выхода оже-электронов,
R - фактор шероховатости поверхности,
T - регистрационная эффективность
энергоанализатора.
Зависимость сечения
ионизации электронным ударом различных атомных уровней достаточно хорошо
изучена как теоретически, так и экспериментально. Характерной чертой этой
зависимости является резкое возрастание сечения вблизи порога ионизации,
равного энергии связи остовного уровня. После достижения максимума при энергии
в 3 - 4 раза, превышающей пороговую, сечение ионизации медленно уменьшается.
Основной
теоретической формулой для полного сечения ионизации внутренних оболочек атомов
электронным ударом является формула Бете [1]:
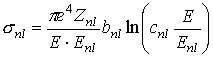 , (7.2)
, (7.2)
здесь Enl – энергия связи электронов;
Znl– число электронов в
оболочке с квантовыми числами n, l. Параметры bnl и cnl отличаются для разных
оболочек атома.
Универсальный
вид, одинаковый для всех элементов, эта формула примет, если ввести
нормированную энергию первичных электронов 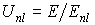 , а сечение ионизации умножить на квадрат энергии связи
электронов:
, а сечение ионизации умножить на квадрат энергии связи
электронов:
 . (7.3)
. (7.3)
Левая часть формулы (7.3) имеет размерность см2×эВ2.
В
литературе часто применяются модификации формулы Бете – формула Грижинского
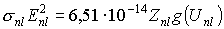 , (7.4)
, (7.4)
 ,
,
и формула Лотца
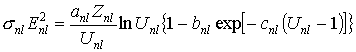 . (7.5)
. (7.5)
Наиболее часто для сравнения
экспериментальных результатов с теоретическими используют формулу Грижинского.
На рис. 7.1. Приведена зависимость сечения ионизации в относительных единицах,
рассчитанная по этой формуле от относительной энергии ионизации. Точками
обозначены экспериментальные результаты для некоторых элементов [2].
Важным
источником дополнительной ионизации остовных уровней и соответствующего выхода
оже-электронов являются рассеянные назад вторичные электроны, создаваемые в
твердом теле первичным пучком. Использование первичных электронов с энергией 3
- 5 кэВ для возбуждения атомных уровней с энергиями связи до 1,5 кэВ приводит к
тому, что многие неупруго рассеянные электроны имеют энергию, достаточную для
ионизации остовных уровней, что приводит к дополнительной эмиссии
оже-электронов. Для мелких уровней этот источник может быть главным источником
ионизации.
Количественной
мерой дополнительной ионизации является коэффициент обратного рассеяния r, который
показывает, насколько увеличивается величина выхода оже-электронов
соответствующего энергетического уровня данного атома по отношению к идеальному
случаю, когда возбуждение поверхностного слоя осуществлялось бы только
первичными электронами.
Экспериментальная
зависимость коэффициента обратного рассеяния от относительной энергии первичных
электронов U для различных элементов приведены
на рис. 7.2. Абсолютная величина энергии первичных электронов менее 2 кэВ [3].
Глубина
выхода или средняя длина свободного пробега оже-электрона зависит от его
энергии и атомной плотности образца N.
Наиболее удовлетворительное
согласие с многочисленными экспериментальными
данными дается выражением
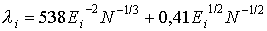 , (7.6)
, (7.6)
где li измеряется в нанометрах, Еi - в электронвольтах.
Совершенно
очевидно, что расчет всех параметров, приведенных в уравнении (7.1), довольно
сложен и сопряжен с большими ошибками. Поэтому, на практике пытаются осуществить
замену возможно большого числа переменных константами и калибруют сигналы от
атомов различного сорта для известных (стандартных) поверхностей. Наиболее
простой и наиболее распространенный приближенный метод количественного анализа
в электронной оже-спектроскопии - метод коэффициентов элементной чувствительности.
Отправной
точкой метода коэффициентов элементной чувствительности является допущение, что
интенсивность оже-сигнала Iiэлемента i
пропорциональна его концентрации на поверхности Xi. Это соответствует замене всех сомножителей в
уравнении (7.1), кроме Xi
, константой Si:
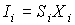 . (7.7)
. (7.7)
Константа Si
определяет чувствительность метода к данному элементу и поэтому ее называют коэффициентом элементной чувствительности.
Коэффициенты элементной чувствительности можно определить из атласов эталонных
спектров чистых элементов, таких, например, как [4]. Все спектры в этом атласе
сняты в идентичных условиях и перед записью каждого спектра производилась
калибровка по сигналу серебра с энергией 351 эВ. Для каждого спектра указана
чувствительность спектрометра. В этом случае коэффициент элементной
чувствительности определяется по формуле
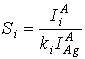 , (7.8)
, (7.8)
здесь 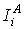 - амплитуда оже-пика
элемента i в атласе,
- амплитуда оже-пика
элемента i в атласе,
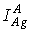 - амплитуда оже-пика Ag (351 эВ) в этом же атласе,
- амплитуда оже-пика Ag (351 эВ) в этом же атласе,
ki - чувствительность
спектрометра, указанная в атласе (для серебра kAg
= 1).
Поскольку
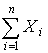 , где n - число элементов в исследуемой системе, то из (7.7)
получим формулу для вычисления концентраций элементов на поверхности.
, где n - число элементов в исследуемой системе, то из (7.7)
получим формулу для вычисления концентраций элементов на поверхности.
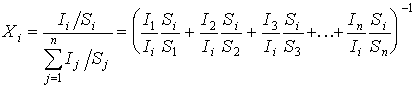 . (7.9)
. (7.9)
7.2. Применение электронной спектроскопии для
изучение механизмов роста тонких пленок
Электронная
оже-спектроскопия и рентгеновская фотоэлектронная спектроскопия широко
применяются для изучения механизмов роста тонких пленок in situ. В этом случае
исследуют характеристики пиков оже-переходов (ЭОС) или пиков фотоэлектронов
(РФЭС) атомов подложки и пленки в зависимости от степени покрытия подложки
материалом пленки. Метод исследования основан на том факте, что число
электронов, дающих вклад в интенсивность соответствующей линии спектра, зависит
от расположения атомов материала, через который эти электроны проникают после
того, как они покинут атомы подложки или адсорбированной пленки. Независимо от
способа возбуждения интенсивность сигнала I, прошедшего сквозь пленку, зависит от средней длины свободного пробега
электронов при определенной энергии и количества материала, через который они
проходят. В зависимости от механизма роста интенсивности сигналов от пленки и
подложки будет по-разному зависеть от степени покрытия пленкой подложки.
Рассмотрим
послойный рост или рост Франка ван дер
Мерве (FM) (см. раздел III,
пункт 3.2). В первом приближении уменьшение интенсивности dI спектральной линии
электронов от подложки прямо пропорционально толщине нанесенной пленки dh[5]:
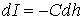 .
.
В
этом случае наблюдается экспоненциальное уменьшение сигнала от подложки ISс увеличением толщины пленки
h:
 , (7.10)
, (7.10)
здесь IS0
– интенсивность линии с чистой поверхности подложки, d –
толщина монослоя пленки, n – число монослоев.
Для
интенсивности линии от пленки IF имеем
 , (7.11)
, (7.11)
здесь IF¥- интенсивность линии объемного
чистого материала.
Тонкую
структуру зависимости сигнала от подложки дает анализ изменения интенсивности
пика в процессе последовательного заполнения каждого слоя растущей пленкой.
Основная идея этого анализа состоит в том, что сигнал подложки, не полностью
покрытой монослоем другого элемента со степенью покрытия q,
описывается простой суммой неослабленной эмиссии с 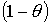 доли поверхности
подложки и ослабленной эмиссии с q доли поверхности подложки
[2,6]. При этом предположении:
доли поверхности
подложки и ослабленной эмиссии с q доли поверхности подложки
[2,6]. При этом предположении:
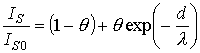 , (7.12)
, (7.12)
Первое слагаемое в этом
выражении описывает вклад в сигнал свободной поверхности подложки, а второе
слагаемое – вклад от той части поверхности подложки, которая закрыта одним
слоем пленки.
Преобразовывая (7.12) к виду
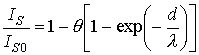
получим, что в диапазоне 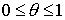 зависимость
интенсивности спектральной линии подложки от степени покрытия qлинейна.
зависимость
интенсивности спектральной линии подложки от степени покрытия qлинейна.
В
процессе роста второго слоя дополнительное ослабление сигнала подложки этим
слоем, степень заполнения которого q, приводит к следующему
соотношению:
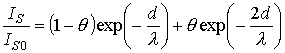 . (7.13)
. (7.13)
Здесь 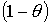 и q обозначают какая часть
поверхности покрыта соответственно одним и двумя слоями. q, также как и в выражении
(7.12), изменяется от 0 до 1. На этой фазе роста зависимость сигнала подложки
также имеет линейный характер, однако, наклон прямой иной, чем для первого
слоя.
и q обозначают какая часть
поверхности покрыта соответственно одним и двумя слоями. q, также как и в выражении
(7.12), изменяется от 0 до 1. На этой фазе роста зависимость сигнала подложки
также имеет линейный характер, однако, наклон прямой иной, чем для первого
слоя.
Последовательно
применяя приведенные выше рассуждения для пленки, соcтоящей из (n+1)
атомных слоев, придем к следующему общему выражению:
 . (7.14)
. (7.14)
Здесь  ,
,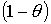 часть поверхности, покрытая n слоями, q - часть поверхности, покрытая (n+1) слоем.
часть поверхности, покрытая n слоями, q - часть поверхности, покрытая (n+1) слоем.
График
зависимости, представленный выражением (7.14) представляет ломаную линию,
состоящую из отрезков прямой, вершины которой лежат на экспоненте,
соответствующей выражению (7.10) (рис.7.3, кривая 1).
В
случае образования монослоя и островков
или роста Странски-Крастанова (SK)
ослабление сигнала от подложки при заполнении первого слоя, так же как и в
случае послойного роста, определяется соотношением (7.12). На второй стадии
роста, когда происходит образование островков, ослабление сигнала подложки
зависит от доли поверхности, покрытой островками. Например, если островки
высотой в 2 слоя покрывают 50% поверхности первого слоя, то
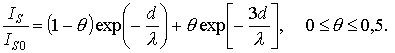 . (7.15)
. (7.15)
Сравнивая, полученное выражение с формулой для
послойного роста, видим, что в случае роста SK кривая 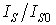 пойдет выше экспоненциальной зависимости и не будет
стремиться к нулю с ростом числа слоев. Схематично кривая затухания для
механизма роста Странски-Крастанова представлена кривой 2 на рис. 7.3.
пойдет выше экспоненциальной зависимости и не будет
стремиться к нулю с ростом числа слоев. Схематично кривая затухания для
механизма роста Странски-Крастанова представлена кривой 2 на рис. 7.3.
![Подпись:
Рис. 7.3. Нормированный выход оже-электронов подложки как функция средней толщины покрытия [6]:
1 – послойный рост; 2 – монослой с островками; 3 – островки, покрывающие 50% поверхности.
Средняя длина свободного пробега l равна двум монослоям.
ep – первичный электрон; eo - оже-электрон.](./Appl.files/image061.gif)
Экспериментальные и
теоретические исследования механизма роста Странски-Крастанова показывают, что
в большинстве случаев амплитуда сигнала уменьшается (от подложки) или
увеличивается (от пленки) линейно до толщины одного слоя (иногда нескольких
слоев), а затем меняется незначительно. В качестве примера на рис. 7.4
приведены экспериментальные зависимости выхода оже-электронов от толщины
покрытия в случае свинцовой пленки на подложке Cu (100) [6]. Шкала для
нормированного значения интенсивности оже-сигнала от меди приведена слева.
Кривая 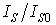 имеет излом вблизи толщины покрытия, равной 1-2 слоям, а
затем очень медленно меняется с увеличением q. Выход оже-электронов для Pb (шкала на рис. 7.4 справа в
произвольных единицах) также достигает насыщения для этих же значений толщины
покрытия. Эти результаты характерны для типа роста Странски-Крастанова.
имеет излом вблизи толщины покрытия, равной 1-2 слоям, а
затем очень медленно меняется с увеличением q. Выход оже-электронов для Pb (шкала на рис. 7.4 справа в
произвольных единицах) также достигает насыщения для этих же значений толщины
покрытия. Эти результаты характерны для типа роста Странски-Крастанова.
Для роста с образованием островков (рост
Вольмера-Вебера) выход электронов из подложки еще выше, чем в механизме
Странски-Крастанова, поскольку некоторая часть подложки остается непокрытой
пленкой. Качественно зависимость интенсивности линии подложки в спектре
электронов от степени покрытия для этого механизма роста представлена на рис.
7.3 кривой 3. Рост чистых островков встречается не так часто, как первые два
типа. Экспериментальное разделение результатов относящимся к механизмам роста Странски-Крастанова
и Вольмера-Вебера встречает большие трудности. Как правило, требуются
дополнительные методы исследования для разделения этих типов роста.
7.3. Влияние химического состояния
элементов на электронные спектры
Химическое
окружение атома существенно влияет на точное значение энергии связи электрона в
этом атоме. Это изменение, которое принято называть химическим сдвигом, вызывается электростатическим взаимодействием
между валентными и внутренними электронами атома. Качественная картина химического
сдвига может быть объяснена в рамках простой модели зарядового потенциала
[2,6]. Энергия электрона во внутренней оболочке определяется кулоновским
взаимодействием с другими электронами и ядром. Любое изменение в химическом
окружении элемента будет влиять на пространственное перераспределение заряда
валентных электронов данного атома и вызывать изменение потенциала, заметное
для внутреннего электрона. Это приводит в конечном итоге к изменению его
энергии связи.
Количественной
мерой химического сдвига является разность 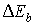 между энергией связи электронов в соединении (молекуле)
между энергией связи электронов в соединении (молекуле)  и в свободном атоме или чистом компоненте
и в свободном атоме или чистом компоненте  :
:
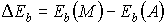 , (7.16)
, (7.16)
В
простейшей модели описания явления химического сдвига валентные электроны
смещаются к ядру или от него в зависимости от типа связи. Чем выше
электроотрицательность (способность присоединять электрон) окружающих атомов,
тем больше смещение электронного заряда от центра атомов и тем выше наблюдаемые
сдвиги энергии связи внутренних электронов.
Для
количественных оценок величину химического сдвига остовных уровней обычно
связывают с изменением эффективного заряда атома в соединении по сравнению с
чистым элементом [7]:
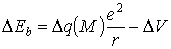 , (7.17)
, (7.17)
здесь 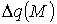 - изменение
эффективного заряда атома А при образовании соединения М:
- изменение
эффективного заряда атома А при образовании соединения М:
 ;
;
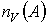 - число валентных
электронов атома А в свободном состоянии;
- число валентных
электронов атома А в свободном состоянии; 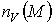 - число валентных
электронов атома А в соединении М; e – заряд электрона; r – радиус валентной
оболочки; член
- число валентных
электронов атома А в соединении М; e – заряд электрона; r – радиус валентной
оболочки; член 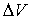 учитывает
взаимодействие электронов атома А с ядром и электронами всех
атомов в соединении.
учитывает
взаимодействие электронов атома А с ядром и электронами всех
атомов в соединении.
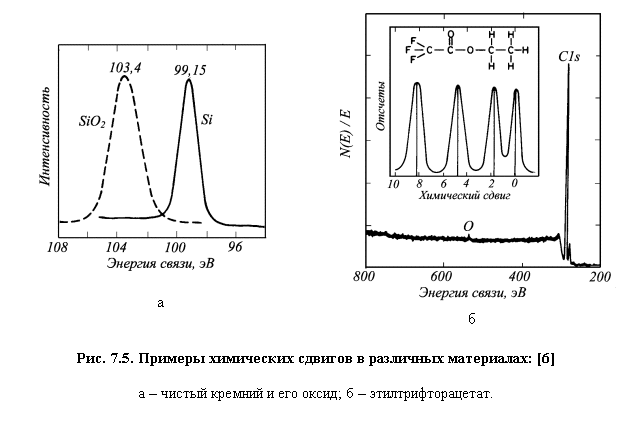
Примеры влияния химических сдвигов
на фотоэлектронные спектры для неорганических и органических соединений
приведены на рис. 7.5. Для чистого кремния энергия связи Si2p уровня составляет 99,15 эВ (рис. 7.5а). Для соединения кремния
с кислородом (SiO2) в соответствии с приведенными выше качественными
оценками, энергия связи Si2p уровня увеличивается
(кислород забирает в силу большой электроотрицательности электроны у кремния).
Экспериментальные значения энергии связи для Si2p уровня оксида кремния
составляет 103,4 эВ. Химический сдвиг составляет более 4 эВ.
На
рис. 7.5б приведен пример химического сдвига в органическом соединении –
этилтрифторацетате (С4F3O2H5). Структурная формула этого соединения, приведенная
на этом же рисунке, свидетельствует о том, что каждый из четырех атомов углерода
находится в различном химическом окружении. Вследствие этого отличаются
химические сдвиги в этих атомов, которые приводят к экспериментально
наблюдаемым четырем фотоэлектронным линиям С1s, положения которых
отличаются приблизительно на 8 эВ.
Для
большинства соединений металлов химические сдвиги значительно меньше, чем в
приведенных выше примерах. В таблице 7.1 приведены данные по энергиям связи и
химическим сдвигам для интерметаллических соединений Ni3Ме (Ме = Ti,Ta, Nb, Mo) и окисла никеля [7].
Таблица 7.1
Энергии связи и химические сдвиги в
различных соединениях никеля
Соединение
|
Ni
|
Ni3Ti
|
Ni3Nb
|
Ni3Ta
|
Ni3Mo
|
NiO
|
|
Eb, эВ
|
852,9
|
852,0
|
852,4
|
852,5
|
852,7
|
854,8
|
|
DEb, эВ
|
-
|
-0,9
|
-0,5
|
-0,4
|
-0,2
|
+1,9
|
Приведенные в таблице данные
могут быть объяснены в рамках рассматриваемой модели перераспределением
электронной плотности в зависимости от донорно-акцепторных свойств компонентов.
Значения химических сдвигов,
даже в пределах десятых долей электронвольта вполне могут быть зарегистрированы
в фотоэлектронных спектрах. Первоначально рентгеновская фотоэлектронная
спектроскопия и развивалась с целью применения этого метода для анализа
соединений по химическим сдвигам фотоэлектронных линий. Об этом говорит и
первоначальное, теперь уже устаревшее название метода – электронная спектроскопия для химического анализа (ЭСХА).
Поскольку кинетическая
энергия оже-электронов, так же как и фотоэлектронов, зависит от энергии
электронных оболочек атома, то химическое окружение атома будет влиять и на
спектр оже-электронов. Однако, в оже-процессах, где участвуют несколько
электронов, химические сдвиги интерпретировать намного труднее, чем в
одноэлектронных фотоэлектронных процессах.
В общем случае кинетическая
энергия оже-электронов для перехода ABC
можно записать в виде (сравнить с формулой 5.2, разд. V):
 , (7.18)
, (7.18)
здесь энергии 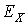 ,
, 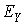 и
и 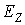 атомных уровней X, Y и Z соответственно, совпадают
со значениями, измеренными в фотоэлектронной спектроскопии, а энергия U
учитывает взаимодействие дырка-дырка. Изменения кинетической энергии
оже-электронов, следовательно, могут быть связаны как с изменением энергий
атомных уровней X, Y и Z соответственно, совпадают
со значениями, измеренными в фотоэлектронной спектроскопии, а энергия U
учитывает взаимодействие дырка-дырка. Изменения кинетической энергии
оже-электронов, следовательно, могут быть связаны как с изменением энергий  ,
, 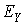 и
и 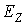 , как в фотоэлектронной спектроскопии, так и с изменением
энергии U.
, как в фотоэлектронной спектроскопии, так и с изменением
энергии U.
Другая причина сложности
интерпретации химических сдвигов в ЭОС связана с тем, что оже-линии в спектрах
вторичных электронов намного шире, чем фотоэлектронные линии.
Тем не менее, в последнее
время все больше исследователей занимаются изучением природы сдвигов энергии
оже-электронов, использование различий в положении и форме оже-линий для
идентификации химического окружения атома данного элемента. Интерес к этим
исследованиям связан с тем, что для некоторых элементов, несмотря на достаточно
большую ширину пика оже-электронов, химические эффекты настолько велики, что
позволяют идентифицировать химические связи, сравнивая спектр оже-электронов в
исследуемом материале с соответствующими спектрами в эталонных соединениях.
![Подпись:
Рис. 7.6. Дифференциальный KLL-спектр углерода в различных химических состояниях [8].](./Appl.files/image100.gif) Классическим примером
влияния химического состояния углерода на вид KLLспектра оже-электронов
приведен на рис. 7.6. Спектр отличается не только для чистого кремния и его
различных соединений с металлом и полупроводником, но и для разных кристаллических
модификаций углерода.
Классическим примером
влияния химического состояния углерода на вид KLLспектра оже-электронов
приведен на рис. 7.6. Спектр отличается не только для чистого кремния и его
различных соединений с металлом и полупроводником, но и для разных кристаллических
модификаций углерода.
Значительные
эффекты, связанные с химическим окружением наблюдаются в кремнии. Для чистого
кремния положение SiLVV
пика соответствует приблизительно 92 эВ, в то время как для оксида кремния
положение этого пика смещается до 70 эВ [8]. Рис. 7.7. иллюстрирует изменение
структуры и увеличение сдвига пика оже-электронов для Si в сторону низких энергий по
мере увеличения электроотрицательности связи [2]. Для чистого кремния,
характеризующегося связью Si – Si, наблюдается одиночный пик
с небольшими особенностями на низкоэнергетическом склоне. Для оксида кремния,
кроме смещения основного пика в сторону низких энергий, отчетливо наблюдается
дополнительный пик (при более детальном рассмотрении спектр оже-электронов SiO2 состоит из четырех пиков
различной интенсивности). Особенности оже-пиков кремния и его оксида
объясняется расположением остовных энергетических уровней и структурой
валентной зоны [9].
Изучение
низкоэнергетического спектра железа применяется для исследования коррозии и начальных
стадий окисления. Для элементного анализа используют высокоэнергетические LMM-пики Cr (529 эВ), Mn (589 эВ), Fe (703 эВ) и других металлов,
на положение которых не оказывает существенного влияния химические связи атомов
железа. С другой стороны для оже-переходов с участием электронов валентной зоны
(MVV-переход для чистого железа,
например, имеет энергию 47 эВ) химическое состояние атома существенно влияет на
структуру спектра оже-электронов. Благодаря химическим эффектам чистые металлы
и их оксиды легко различаются методом ЭОС по химическим сдвигам и анализу
тонкой структуры низкоэнергетических спектров. Для соединений железа и других
переходных металлов
с кислородом в низкоэнергетической области спектра
оже-электронов наблюдается структура, состоящая, как правило, из двух пиков
разной интенсивности. Анализ энергетического расстояния между ними и
соотношений между их амплитудами позволяет установить однозначную зависимость
между этими характеристиками спектров и химическим состоянием металлов.
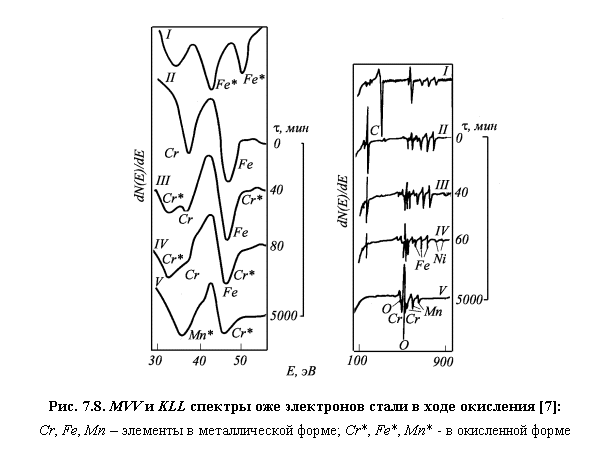
На
рис. 7.8 приведен пример изменения низкоэнергетического MVV и высокоэнергетического KLL оже-спектров нержавеющей
стали в результате окисления при 973 К и давлении кислорода 1·10-4
Па [7]. Исходный KLL-спектр I
свидетельствует о наличие поверхностного слоя загрязнений: в спектре
присутствуют достаточно интенсивные пики углерода и кислорода. После очистки в
результате ионного травления (спектр II) в спектрах присутствуют
оже-линии хрома, железа и никеля от чистой металлической поверхности. По мере
окисления в высокоэнергетическом спектре уменьшаются линии железа,
увеличиваются линии марганца, хрома и кислорода. Низкоэнергетический спектр
указывает на превращение металлического хрома в окисел, в то время как железо
остается в металлическом состоянии.
7.4. Послойный анализ методами электронной спектроскопии
Высокая
поверхностная чувствительность методов электронной спектроскопии, позволяющая
зондировать только верхние очень тонкие слои поверхности, дает возможность
использовать эти методы для трехмерного анализа, обладающего высоким
пространственным разрешением в направлении, перпендикулярном поверхности. Такой
анализ, часто называемый послойным
или профилированием по глубине,
находит широкое применение при технологическом контроле мультислойных
полупроводниковых и магнитных структур, интегральных микросхем, различных
покрытий и др.
Методы,
применяемые для послойного анализа, зависят от соотношения толщины исследуемого
слоя и длины свободного пробега электронов. Когда глубина профилирования
сопоставима с длиной свободного пробега электронов, применяют неразрушающие
методы послойного анализа, основанные на том, что длина свободного пробега
регистрируемых электронов существенно зависит от их кинетической энергии. Для
электронов с энергией 100 и 2000 эВ средняя длина свободного пробега
увеличивается приблизительно в 6 раз (см. разд.VI, рис. 6.2). В ряде случаев
энергию регистрируемых электронов можно изменять, варьируя кинетическую энергию
первичных электронов. Энергия электронных пиков, например, обусловленных потерями
энергии на ионизацию внутренних уровней атомов, смещаются в электронном спектре
вместе с упругим пиком. С ростом энергии первичных электронов в этом случае
увеличивается информация по глубине. На рис. 7.9 представлены спектры края
поглощения Si2sдля образца кремния,
покрытого тонкой пленкой оксида, для разных энергий первичных электронов [7].
Для энергии 500 эВ линия чистого кремния имеет меньшую интенсивность, чем линия
оксида. С увеличением энергии первичных электронов относительная интенсивность
пика чистого кремния заметно возрастает.
Другая
возможность неразрушающего послойного анализа связана с измерением зависимости
сигнала от угла регистрации эмитированных электронов. Идея этого метода связана
с тем, что при регистрации вторичных электронов, эмитированных под углом j относительно нормали к поверхности образца,
в выражении (7.1) необходимо вместо средней длины свободного пробега электронов
в образце учитывать «эффективную» глубину выхода, которая, очевидно, равна


 . (7.19)
. (7.19)
Применение
этого метода ограничено специальными требованиями к аппаратуре и связано с
необходимостью изменения угла регистрации эмитированных электронов.
Для
профилирования слоев, толщина которых значительно превышает среднюю длину
свободного пробега электронов, необходимо применять разрушающие методы
послойного анализа. Для достаточно большой глубины профилирования (порядка
нескольких микрон) используют метод косого шлифа или его модификации: послойный
анализ на краю кратера травления или послойный анализ с использованием шаровых
шлифов [2]. В этих методах механическим способом создается наклонный срез
слоистой структуры, что позволяет перемещением хорошо сфокусированного
электронного луча в плоскости образца смещаться к слоям расположенным на разной
глубине от поверхности. В методе косого шлифа необходимо использовать технику
прецизионного съема материала под углами порядка 10º, связанную со
специальными способами шлифования [7]. На рис. 7.10 приведен пример
профилирования этим методом полупроводниковой сверхрешетки InP/GaInAs, толщиной приблизительно 1 мкм. Внизу представлена
схема структуры: x и z – координаты вдоль
плоскости и перпендикулярно плоскости сверхрешетки соответственно. Вверху
приведен профиль интенсивности оже-пика фосфора в зависимости от координаты x. Этот метод позволяет
исследовать неоднородности порядка 3,5 нм [7].
Универсальным
разрушаемым методом послойного анализа является сочетание одного из методов
электронной спектроскопии, например, электронной оже-спектроскопии или рентгеновской
фотоэлектронной спектроскопии с ионным травлениям. Для этого практически все
электронные спектрометры снабжены ионной пушкой, которая позволяет не только
очищать поверхность от посторонних примесей, но и производить профилирование по
глубине. Высокоэнергетический ион, в 
результате
многократных столкновений с атомами, расположенными на поверхности твердого
тела (рис. 7.11), передает им часть своей кинетической энергии. Если эта
энергия превосходит энергию связи атомов с поверхностью, то процесс ионной
бомбардировки сопровождается удалением атомов или даже групп атомов с
поверхности, в результате чего для зондирования открываются более глубокие
атомные слои структуры. Выбивание иона, отдельного нейтрального атома или
атомного кластера происходит в результате каскада многократных столкновений
между внедренным ионом и частицами твердого тела.
Продукты распыления также
могут быть проанализированы для определения состава распыляемого вещества.
Анализ распыленных ионной бомбардировкой ионов лежит в основе распространенного
метода исследования поверхности – вторичной
ионной масс-спектрометрии (ВИМС).
Эффективность
процесса ионного распыления определяется количественной характеристикой –
коэффициентом распыления Y,
который равен числу распыленных атомов на один падающий ион. Коэффициент
распыления зависит от сорта ионов и распыляемых атомов, состояния мишени (для
монокристаллических и поликристаллических поверхностей и даже для поверхностей
различной кристаллографической ориентации коэффициент распыления существенно
отличается). Диапазон значений коэффициента распыления для ионов средней массы
с энергией в несколько килоэлектронвольт , наиболее часто применяемых для
изучения профилей, лежат между 0,5 и 20 [6]. Теоретические модели процесса
взаимодействия ионов высокой энергии с веществом, использующих механизм ядерных
потерь энергии, достаточно хорошо предсказывают значения коэффициентов
распыления только для простых однокомпонентных веществ.
Зависимость коэффициента
распыления от сорта атомов мишени приводит к существенному недостатку этого
способа послойного анализа – избирательному травлению, сопровождающемуся
постепенным обогащением поверхности одним из элементов. Для многокомпонентных
систем выход отдельных элементов определяется парциальным коэффициентом
распыления данного элемента Yi, который пропорционален концентрации этого элемента
на поверхности. Для двухкомпонентной системы отношение парциальных
коэффициентов распыления элементов A и B равно [6]
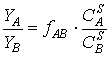 , (7.20)
, (7.20)
здесь 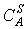 и
и 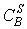 - концентрации
соответственно элементов A и B на поверхности;
- концентрации
соответственно элементов A и B на поверхности;  - множитель,
учитывающий различия поверхностных энергий связи, глубин выхода распыленных
частиц и передаваемых в каскаде энергий. Если
- множитель,
учитывающий различия поверхностных энергий связи, глубин выхода распыленных
частиц и передаваемых в каскаде энергий. Если  > 1, то происходит преимущественное
травление элемента A и
поверхность обогащается элементов B.
> 1, то происходит преимущественное
травление элемента A и
поверхность обогащается элементов B.
Другая
причина, затрудняющая интерпретацию результатов послойного анализа, связана с
тем, что процесс распыления далек от идеального послойного стравливания верхних
атомных слоев. Этот процесс сопровождается перемешиванием атомов в пределах
каскада столкновений, выбиванием атомов из второго слоя, до тех пор, пока не
завершено удаление предыдущего слоя, диффузией атомов и др. Результатом этих
процессов будет дополнительное уширение границ раздела между слоями с разным
элементным составом. Эффект дополнительного уширения можно свести к минимуму
выбором энергии первичных ионов, угла падения, вращением образца и т.д.
|
|
![Подпись:
Рис. 7.12. Профили концентраций многослойной тонкопленочной структуры Cr/Ni, осажденной на кремниевую подложку [6]:
1 – никель; 2 – хром; 3 – кремний.](./Appl.files/image122.gif) |
Конечной информацией, получаемой при
послойном анализе, является зависимость концентрации элементов, составляющих
исследуемую слоистую структуру от глубины. Для решения этой задачи необходимо
не только получить, измеряемый методами электронной спектроскопии, профиль концентраций,
но и, учитывая искажения этого профиля в результате ионного травления, выявить
первоначально существовавший профиль концентраций. Этапы решения этой задачи
подробно изложены в [2].
В
качестве примера применения метода послойного распыления на рис. 7.12 приведен
профиль многослойной структуры Cr/Ni, осажденной на кремниевую
подложку [6]. Верхний слой никеля имел толщину около 250 Å, остальные
слои Ni и Сr – 500 Å. Верхний
рисунок представляет профиль концентраций Ni, Cr и Si для неподвижного образца. С
увеличением времени распыления возрастает закругленность графиков концентраций,
что связана с возрастанием неровности поверхности под влиянием ионного
травления. Вращение образца приводит к более однородному распылению, что
отражается в более резких границах раздела между слоями никеля и хрома.
Литература
1. Валиев
К.А. Физика субмикронной литографии.- М.: Наука. 1990.- 528 с.
2. Анализ
поверхностиметодами
оже- и рентгеновской фотоэлектронной спектроскопии / Под ред. Д. Бриггса, М.П.
Сиха.- М.: Мир, 1987.- 600 с.
3. Применение
электронной спектроскопии для анализа поверхности: пер с англ. / Ж.Д. Карет, Б.
Фейербахер, Б. Фиттон и др. Под ред. Х. Ибаха.- Рига: Зинетне, 1980.- 315 с.
4.
Davis
L.E., MacDonald N.C. et al., Handbook of Auger Electron Spectroscopy, 2nd edition,
Physical Electronics inc., Eden Prarie, Minn, 1976.
5.
Luth
H. Surfaces and Interfaces of Solids,
Second Edition, Springer Verlag, Berlin Heidelberg, 1993. - 487 p.
6. Фельдман
Л., Майер Д. Основы анализа поверхности и тонких пленок.- М.: Мир, 1989.- 564.
7. Ковалев
А.И., Щербединский Г.В. Современные методы исследования поверхности металлов и
сплавов.- М.: Металлургия, 1989.- 192 с.
8. Вудраф
Д., Делчар Т. Современные методы исследования поверхности.- М.: Мир, 1989.- 564
с.
9.
Madden
H.H. Auger lineshape analysis // Surface Science.- 1983.- Vol 126, No.1.- p.
80-100.
![]() , (7.1)
, (7.1)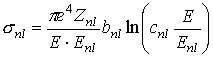 , (7.2)
, (7.2)![]() , а сечение ионизации умножить на квадрат энергии связи
электронов:
, а сечение ионизации умножить на квадрат энергии связи
электронов: . (7.3)
. (7.3)![]() , (7.4)
, (7.4) ,
,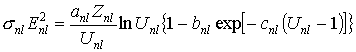 . (7.5)
. (7.5)![Подпись: Рис. 7.1. Зависимость сечения ионизации по Грижинскому от приведенной энергии и результаты экспериментальных измерений для Be, C, Si, Ag и Gd [2]](./Appl.files/image016.gif)
![Подпись:
Рис. 7.2 Зависимость коэффициента обратного рассеяния для нескольких элементов от нормированного значения энергии электронов [3]](./Appl.files/image018.gif)
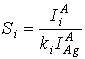 , (7.8)
, (7.8)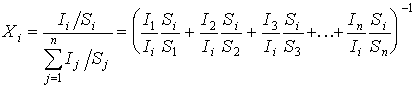 .
.  , (7.10)
, (7.10) , (7.11)
, (7.11)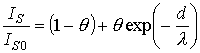 , (7.12)
, (7.12)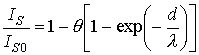
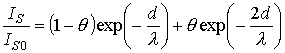 . (7.13)
. (7.13) . (7.14)
. (7.14)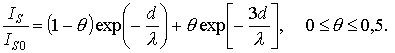 . (7.15)
. (7.15)![Подпись:
Рис. 7.3. Нормированный выход оже-электронов подложки как функция средней толщины покрытия [6]:
1 – послойный рост; 2 – монослой с островками; 3 – островки, покрывающие 50% поверхности.
Средняя длина свободного пробега l равна двум монослоям.
ep – первичный электрон; eo - оже-электрон.](./Appl.files/image061.gif)
![Подпись:
Рис. 7.4. Кривые выхода оже-электронов для роста свинцовой пленки на Cu (100) [6]:
1 - налетающий электрон; 2 – оже-электрон из Pb; 3 – оже-электрон из Cu.](./Appl.files/image063.gif)
![Подпись:
Рис. 7.6. Дифференциальный KLL-спектр углерода в различных химических состояниях [8].](./Appl.files/image100.gif)




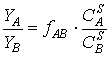 , (7.20)
, (7.20)![Подпись:
Рис. 7.12. Профили концентраций многослойной тонкопленочной структуры Cr/Ni, осажденной на кремниевую подложку [6]:
1 – никель; 2 – хром; 3 – кремний.](./Appl.files/image122.gif)