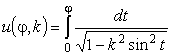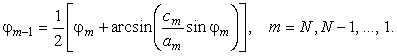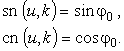Содержание
Введение. 2
1. Общая
теория изгиба стержней. 3
1.1
Криволинейная система координат. 3
1.2 Уравнение равновесия. 4
1.3 Закон Гука. 6
1.4 Уравнение
равновесия в криволинейных координатах. 7
2. Решения
общего уравнения для различных видов граничных условий 9
2.1 Консоль
защемленный конец. Поперечное приложение силы.. 9
2.2.Консоль
защемленный конец. Продольное приложение силы.. 12
2.3 Консоль
защемленный конец. Произвольное приложение силы 13
2.4.
Защемленные концы. Продольное приложение силы.. 15
2.5.
Закрепленные концы. Продольное приложение силы.. 16
3.Алгоритмы
вычислений эллиптических функций и интегралов. 18
3.1
Эллиптические интегралы.. 18
3.2 Метод
арифметико-геометрического среднего. 18
3.2.1 Вычисление полного эллиптического интеграла первого
рода K(k) 18
3.2.2 Вычисление полного эллиптического интеграла второго
рода E(k) 19
3.3 Метод
понижающего преобразования Ландена. 19
3.3.1 Вычисление неполного эллиптического интеграла
первого рода F(j, k) 19
3.3.2 Вычисление неполного эллиптического интеграла
второго рода E(j, k) 20
3.4
Эллиптические функции Якоби. 20
3.4.1 Вычисление эллиптических функций Якоби sn u, cn u. 21
4.Пакет
прикладных программ Elastic Rod. 22
4.1 Структура программы.. 22
Приложение 1. 24
Литература. 29
Задача об изгибе
стержня является одним из вопросов расчета конструкций. Как правило, такие
задачи, решаются на базе приближенных линеаризованных уравнений равновесия для
изогнутых стержней, приводящих к решению в виде полиномов. В основном,
используются эти решения. Вместе с тем имеются для некоторых случаев точные
решения нелинейных уравнений, выраженные в квадратурах [1], или в эллиптических
интегралах [2]. В последнем случае решения определяются тремя параметрами,
связанными с условиями на двух концах и действующей силой и определяющихся из
вспомогательных таблиц и номограмм. Все эти решения имеют громоздкий вид и
труднодоступны для инженеров практиков, поэтому до последнего времени всерьез
решались задачи получения приближенных
выражений даже для таких стандартных характеристик как максимальный прогиб
стержня [5]. Вместе с тем в последнее время был, достигнут
определенный прогресс в получении точных решений, в некоторых случаях
выраженных через эллиптические функции с единственным параметром модулем k,
определяемым действующей силой.
В настоящее время известны достаточно
эффективные, быстрые алгоритмы для вычисления эллиптических функций и интегралов,
что позволяет создать эффективный пакет прикладных программ для расчета изгиба
тонких стержней в точном виде. Это должно иметь ясно выраженное прикладное
инженерное значение при расчете устройств точной механики в условиях
ограниченных габаритов, поскольку точные решения в ряде случаев значительно
отличаются от приближенных. Например: прогиб приближенного решения оказывается
в два раза больше точного. Поэтому сравнение точных решений с приближенными
может позволить найти те области параметров, где целесообразно использовать
точное или возможно использовать приближенное. Это может позволить выбрать
оптимальные характеристики создаваемых устройств в точной механике. Поэтому
необходимо создать такие прикладные пакеты, которые будут просты для применения
любыми пользователями и полезны как тестовые задачи для проверки существующих
решений.
Уравнения изгиба
стержней хорошо известны. Их можно получить вариационным методом или из условия
равновесия моментов сил (см., например, []). Приведем здесь в общем виде теорию
изгиба стержней для случая больших геометрических нелинейностей, следуя Л.Д.
Ландау и Е.М. Лифшицу [1].
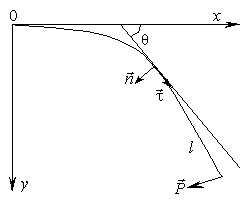
Введем систему
координат. Пусть x, y – декартовы координаты в
плоскости изгиба стержня, l –
длина вдоль линии стержня, θ = θ(l) – угол наклона касательной в текущей точке к линии стержня, а κ
= κ(l) = dθ/dl – кривизна этой кривой.
Отнесем один закрепленный конец стержня в начало координат. Тогда:
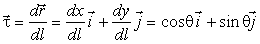 (1)
(1)
– единичный вектор
касательной к кривой l, а
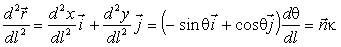
– вектор нормали к кривой, где
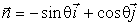 (2)
(2)
– единичный вектор нормали. Таким образом, мы
рассмотрели две системы координат – декартовы координаты, с единичными ортами i и j, и касательную систему
координат, с подвижными вдоль линии стержня (поскольку угол θ(l)
зависит от криволинейной длины l), единичными ортами τ
и n. Единичные орты связаны
между собой единичной матрицей перехода
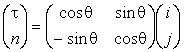 ,
, 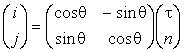 .
.
Соответственно любой вектор А имеет компоненты в каждой системе координат:
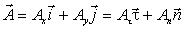 ,
,
которые также связаны между собой этой матрицей
перехода:
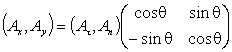 ,
, 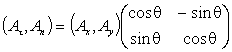 . (3)
. (3)
Производные единичных ортов вдоль кривой связаны
между собой очевидными соотношениями:
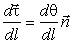 ,
, 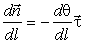 . (4)
. (4)
Линию стержня целесообразно будет задавать в виде
функциональной зависимости θ = θ(l). Тогда линия стержня в параметрическом задании, с параметром
криволинейная длина l,
легко восстанавливается:
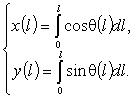 (5)
(5)
1.2 Уравнение
равновесия
Получим
уравнение равновесия тонкого стержня, изгибающегося в плоскости с помощью
уравнений равновесия для каждого малого элемента стержня. Рассмотрим
какой-нибудь из бесконечно малых элементов стержня, вырезанный двумя бесконечно
близкими сечениями, и вычислим полную действующую на него силу. Обозначим
полную силу внутренних напряжений, приложенную к площади сечения стержня,
посредством F. Компоненты этого вектора равны интегралам от напряжений sij по площади сечения:
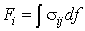 . (6)
. (6)
Если
рассматривать два бесконечно близких сечения как поверхности оснований
вырезаемого ими элемента стержня, то на верхнее основание действует сила F + dF, а на нижнее действует сила
F. Их сумма есть дифференциал
dF. Пусть далее K есть действующая на
стержень внешняя распределенная сила, отнесённая к единице его длины. Тогда на
элемент длины dl действует внешняя сила Kdl. Равнодействующая всех сил,
действующих на этот элемент, есть dF + K dl. В равновесии эта сила
должна обращаться в нуль. Таким образом, получаем
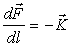 . (7)
. (7)
Второе уравнение
находится из условия равенства нулю полного момента сил, приложенных к данному
элементу. Пусть M есть момент сил внутренних
напряжений, действующих на площадь сечения стержня. Этот момент берется
относительно точки (начала координат), лежащей в самой плоскости этого сечения.
Будем вычислять суммарный момент, приложенный к данному элементу стержня,
относительно точки (назовем ее точкой О),
лежащей в плоскости его верхнего основания. Тогда внутренние напряжения на этом
основании дают момент M + dM. Момент относительно точки О сил внутренних напряжений в нижнем
основании элемента складывается из момента –M этих сил относительно начала
координат в плоскости нижнего основания (точка О¢) и момента относительно О суммарной силы –F, действующей на этом
основании. Этот второй момент равен [(-dr)×(-F)], где dr - вектор элемента длины
стержня от O¢ к O, а r(x, y) - радиус вектор. В равновесии
полный действующий на элемент стержня момент сил должен быть равен нулю: dM + [dr×F] =
0. Разделив это равенство на dl,
получаем уравнение
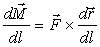 . (8)
. (8)
Уравнения (7) и (8)
представляют собой полную систему уравнений равновесия произвольным образом
изогнутого стержня. Продифференцировав (8), подставим в него (7) и получим
общее уравнение равновесия стержня
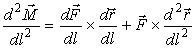 . (9)
. (9)
Рассмотрим стержень изначально не изогнутый и расположенный вдоль
оси ОX (Рис.2). Внешняя распределенная нагрузка отсутствует, К = 0. Левый конец стержня защемлен, на
свободный правый действует сосредоточенная поперечная нагрузка Р, направленная вдоль оси OY, Рy = P, Px = 0.
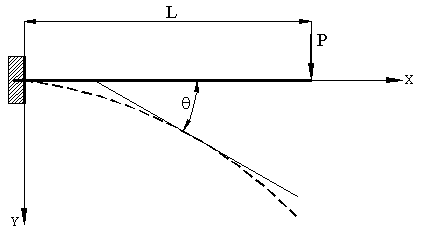
Рис.
2.
Введем новую неизвестную
переменную γ(l) =
θ(l) + π/2. Тогда
уравнение (16) будет в переменных γ(l) иметь вид
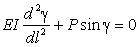 . (17)
. (17)
Это широко известное
уравнение нелинейного маятника. Его общее решение записывается в эллиптических
функциях Якоби
g(l) = 2arcsin[k sn(ql +
c)].
Здесь введено обозначение
собственного числа q = P/EI, модуль k и c – константы интегрирования.
Граничными условиями для уравнения (17) в данной задаче будут выражения:
γ(0) = π/2 – защемление, dγ/dl(L) = 0 – свободный конец.
Спектр собственных значений при этих условиях имеет вид:
P/Pc = (2/p)2{(2n - 1) K(k) - F [arcsin(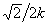 ), k]}2,
n = 1, 2, ... (18)
), k]}2,
n = 1, 2, ... (18)
где Рс = (p/2)2EI/L2 – Эйлерова сила. Координаты x и y произвольной точки стержня
в параметрическом виде (безразмерный параметр t = l / L
изменяется от 0 до 1) записываются следующим образом:
x/L = [2k / (pK - F1)] [(1-1/2k2)1/2 - cnu],
y/L = t - [2/(pK - F1)] [E(amu, k) - E1 ]. (19)
где аргумент u =
(pK - F1)t +F1 cnu и amu - эллиптические косинус и
амплитуда Якоби, E(j, k) - неполный эллиптический интеграл второго
рода, введено обозначение
E [ arcsin(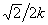 ), k] º E1, и учтено, что cn(F1, k) = cos(arcsin
), k] º E1, и учтено, что cn(F1, k) = cos(arcsin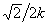 )
= (1 - 1/2k2)1/2.
)
= (1 - 1/2k2)1/2.
Уравнения (19)
описывают в параметрическом виде (0 £ t £ 1) форму сильно изогнутой
консоли под действием статической (n = 1) и динамических (n = 2, 3, ...) нагрузок.
Модуль k изменяется в пределах 1/2 £ k2 £ 1, задает общую кривизну
консоли и определяется действующей силой P.
При этом для каждого порога зависимость k2(P/Pc) определяется своим
уравнением (18) при соответствующем p =
2n - 1.
Форма стержня
при динамической нагрузке перестает быть монотонной кривой. Запишем
характеризующие ее производные
dy/dx = (1 - 2d2) / 2k s d,
d2y/dx2 = (pK
- F1) c / 4Lk2 s3d3.
Здесь
использованы обозначения s = snu, d
= dnu, c = cnu. Точки максимума
и минимума определяются уравнением dnu =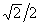 ,
точки перегиба - условием cnu = 0. Здесь учтено, что pK - F1 > 0
всегда, кроме как на статическом, нулевом пороге при p = 1 и P = 0; величина F1 изменяется в пределах K(
,
точки перегиба - условием cnu = 0. Здесь учтено, что pK - F1 > 0
всегда, кроме как на статическом, нулевом пороге при p = 1 и P = 0; величина F1 изменяется в пределах K(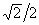 )
³ F1 ³ F(p/4, 1), т.е. 1.85 ³ F1 ³ 0.88. Число точек перегиба
зависит от номера моды p. При p = 1 есть одна точка перегиба при t = 1, что совпадает с широко
используемыми приближенными решениями в виде полиномов. При p = 3 есть две точки перегиба, которые
при 1/2 £ k2 £ 1 лежат в пределах: 0 £ t1 £ 1/3, t2 = 1. При p = 5 есть три точки перегиба: 0 £ t1 £ 1/5, 1/2 £ t2 £ 3/5, t3
= 1. Координаты свободного конца консоли равны (при t = 1):
)
³ F1 ³ F(p/4, 1), т.е. 1.85 ³ F1 ³ 0.88. Число точек перегиба
зависит от номера моды p. При p = 1 есть одна точка перегиба при t = 1, что совпадает с широко
используемыми приближенными решениями в виде полиномов. При p = 3 есть две точки перегиба, которые
при 1/2 £ k2 £ 1 лежат в пределах: 0 £ t1 £ 1/3, t2 = 1. При p = 5 есть три точки перегиба: 0 £ t1 £ 1/5, 1/2 £ t2 £ 3/5, t3
= 1. Координаты свободного конца консоли равны (при t = 1):
x/L = 2k (1 - 1/2k2)1/2 / (pK - F1),
y/L = 1 - 2(pE - E1) / (pK - F1),
где E = E(k) - полный эллиптический
интеграл второго рода.
Для статической
моды p = 1 при нагрузке P®0 модуль k2®1/2, неполные интегралы E(j, k)®E(k),
F(j, k)®K(k). Используя полученные в [] разложения этих неполных
эллиптических интегралов при k2 » 1/2, находим координаты
свободного конца y/L » 2k2 - 1, x/L » (2 - 2k2)1/2
и при k2 = 1/2 координаты y/L = 0, x/L = 1.
Для динамических
мод (p = 3, 5, ...) координаты
свободного конца (t = 1)
x/L = 2k (1 - 1/2k2)1/2 / (p - 1)K,
y/L = 1 - 2E / K,
и на порогах, при k2 = 1/2, отсюда имеем
x/L =
0, y/L
» -0.46 при t =
1
независимо от номера моды.
Рассмотрим стержень изначально не изогнутый и расположенный вдоль
оси ОX (Рис. 3). Внешняя распределенная нагрузка отсутствует, К = 0. Левый конец стержня защемлен, на
свободный правый действует сосредоточенная продольная нагрузка Р, направленная вдоль оси OХ, Рy = 0,
Px = - P.
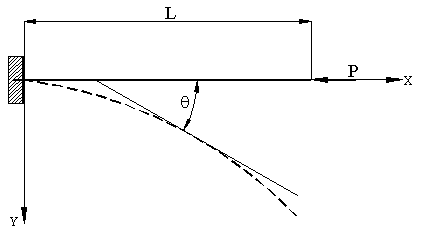
Рис. 3
Уравнение для этого случая
приложения силы принимает следующий вид:
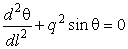 .
.
Граничными условиями для данного уравнения будут
выражения:
q(0) = 0, 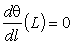 .
.
В этом случае общее решение имеет вид:
q(t) = 2arcsin[k sn(qt + F1, k).
Применив первое граничное
условие, имеем F1 = 2m’K, второе условие q +
2m’K = (2m” –1)K ,
где m’, m” – принимают значения 1, 2,
3, …
По свойству нулей эллиптического
косинуса Якоби получим
q =( 2 m”
–2 m’ - 1 ) K
= p K, где p =2 m –
1 = 1, 3, 5, …
Спектр собственных значений
при этих условиях имеет вид:
P/Pc = (2/p)2{(2n - 1) K(k) }2, n = 1, 2, ...
Координаты х и y в произвольной точке
стержня в параметрическом виде записываются в следующем виде:
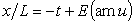 ,
,
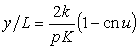 .
.
где аргумент и = pK t,
t – параметр.
Изначально стержень не
изогнут и расположен вдоль оси ОX (Рис. 4). Внешняя
распределенная нагрузка отсутствует, К
= 0. Левый конец стержня защемлен, на свободный правый действует
сосредоточенная нагрузка Р под углом f, где 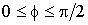 .
.
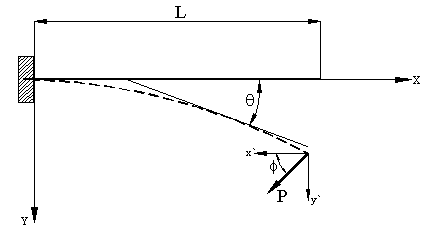
Рис. 4.
Уравнение имеет вид:
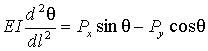 .
.
Подставляя Px = - P cosf, Py = P sinf.
Получаем уравнение в виде
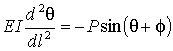 ,
,
введем новую переменную g(l) = q(l) + f, где f - угол приложения силы. Тогда уравнение будет иметь
вид
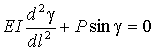 .
.
Общее решение
g = 2
arcsin (k sn(ql +
F1)).
Граничными условиями для данного уравнения будут
выражения:
g(l) = f , dg/dl(L) = 0.
Применив первое граничное условие, имеем sin(f/2) = k sn F1, 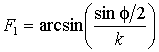 .
Модуль эллиптической функции изменяется в пределах
.
Модуль эллиптической функции изменяется в пределах 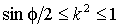 . Первая производная
. Первая производная
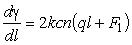 .
.
Применив второе граничное условие, получим:
q = (2m - 1)K – F1. где m =
1, 2, 3, …
Спектр собственных значений при этих условиях имеет
вид:
P/Pc = (2/p)2{(2n - 1) K(k) - F 1}2, n = 1, 2, ...
Линия стержня в параметрическом задании легко
восстанавливается
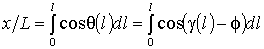 ,
,
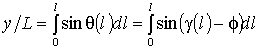 .
.
Координаты x и y в произвольной точке стержня
в параметрическом виде записываются в следующем виде:
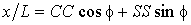 ,
,
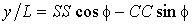 .
.
где введены обозначения
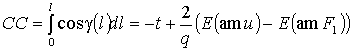 ,
,
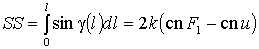
и аргумента u = (pK
– F1) t+ F1.
Рассмотрим
стержень изначально не изогнутый и расположенный вдоль оси ОХ (Рис. 5). Внешняя
распределенная нагрузка отсутствует, К = 0. Стержень защемлен с двух
сторон, на правый конец действует сосредоточенная продольная нагрузка Р,
направленная вдоль оси ОХ, Рх = Р, Ру
= 0.
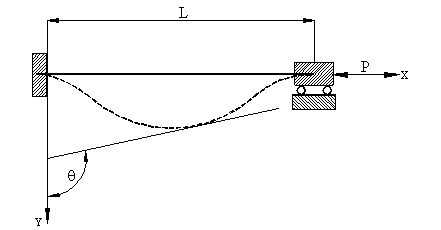
Рис. 5.
Уравнение для этого случая
приложения силы принимает следующий вид:
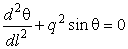 .
.
Граничными условиями для данного уравнения будут
выражения:
q(0) = 0, q(1) = 0,..
В этом случае общее решение имеет вид:
q(t) = 2arcsin[k sn(qt + F1, k).
Применив первое граничное
условие, имеем F1 = 2m’K, второе условие q +
2m’K = 2m” K ,
где m’, m” – принимают значения 1, 2,
3, …
По свойству нулей
эллиптического косинуса Якоби получим
q =2( m”
– m’ ) K = 4 m K, где m =
1, 2, 3, …
Спектр собственных значений
при этих условиях имеет вид:
P/Pc = (2/p)2{(
4 n K(k) }2, n = 1, 2, ...
Координаты х и y в произвольной точке
стержня в параметрическом виде записываются в следующем виде:
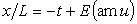 ,
,
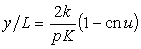 .
.
где аргумент и = 4pK t,
t – параметр.
Рассмотрим
стержень изначально не изогнутый и расположенный вдоль оси ОХ (Рис. 6). Внешняя
распределенная нагрузка отсутствует, К = 0. Стержень шарнирно закреплен
с двух сторон, на правый конец действует сосредоточенная продольная нагрузка Р,
направленная вдоль оси ОХ, Рх = Р, Ру
= 0.
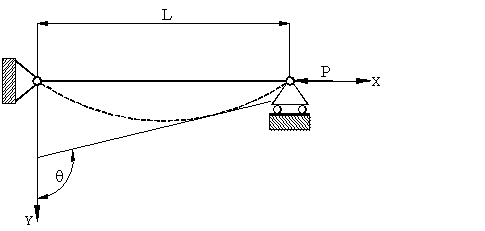
Рис. 6.
Уравнение имеет вид
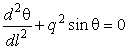 .
.
Общее решение
q(t) = 2arcsin[k sn(qt + F1, k),
где введено обозначение для неполного эллиптического
интеграла первого рода F1 = F [arcsin(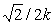 ), k].
), k].
Граничными условиями для уравнения в данной задаче
будут выражения:
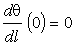 ,
, 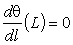 .
.
Первая производная
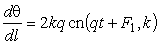 .
.
Применив первое граничное условие, имеем F1 = (2 n’ + 1)K,
второе условие
q + F1 = (2 n’’ + 1)K,
где n’, n” – принимают значения 1, 2,
3, …
По свойству нулей
эллиптического косинуса Якоби получим
q = 2 ( n’ - n” )K =
2 mK , где m = 1, 2, 3… спектр собственных чисел.
Спектр собственных значений
при этих условиях имеет вид:
P/Pc = (2/p)2{2nK(k)}2,
n = 1, 2, ...
Координаты х и y в произвольной точке стержня
в параметрическом виде записываются в следующем виде:
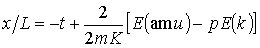 ,
,
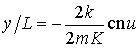 ,
,
где аргумент u =
2 pK t
В случае разложения по малым k
приходим к следующим выражениям силы и координат изогнутого стержня:
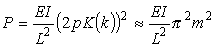
k » 0, y(x) = sin(mpx/L),
что соответствует приближенным решениям приведенным у А. С. Вальмира [6] для
данного вида закрепления.
Эллиптическим в
общем случае называется интеграл:
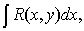
где R (x,
y)- рациональная функция от х, у.
Эллиптический интеграл
первого рода:
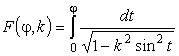 .
.
Эллиптический интеграл
второго рода:
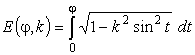 .
.
Здесь j - амплитуда; k – модуль эллиптического
интеграла.
Интегралы, у которых
амплитуда j = p/2, называются полными. Для интегралов
первого и второго рода применяются обозначения
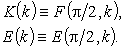
Если модуль вещественный, то
без ограничения общности можно считать, что k £ 1. Используется также дополнительный
модуль, равный по определению
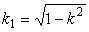 .
.
При вычисление K(k)
одним из наиболее эффективных является итерационный метод арифметико-геометрического
среднего (АГС). Начиная с пары чисел a0 = 1, b0
= k1 = cos a, находятся следующие
среднее арифметическое и среднее геометрическое, которые образуют две
сближающиеся последовательности:
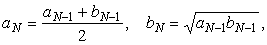
Процесс заканчивается при
таком N, для
которого aN = bN c заданной точностью. Искомое значение K(k)
определяется по формуле
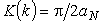 .
.
Требуемые значения N растут
по мере приближения k к единице, а k1 к нулю.
Вычисление полного
эллиптического интеграла второго рода производится
по той же схеме АГС с использованием разностей
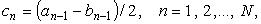
получаемых на каждой итерации. Тогда
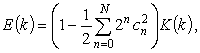
где с0 = k.
Вычистить неполный
эллиптический интеграл F(j, k) можно с помощью понижающего
преобразования Ландена, при котором производится последовательный переход к
эллиптическим интегралам с прогрессивно уменьшающимся модулем. Модуль,
амплитуда и интеграл преобразуются следующим образом:
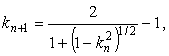
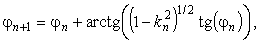
Выбирается ветвь arctg,.
Для которой 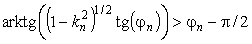 . N – кратное повторение
указанного преобразования должно привести к эллиптическому интегралу F(jN, kN) с настолько малым aN, что F (jN, kN) » jN. Возвращение обратным
преобразованием к старому значению j приводит к формуле
. N – кратное повторение
указанного преобразования должно привести к эллиптическому интегралу F(jN, kN) с настолько малым aN, что F (jN, kN) » jN. Возвращение обратным
преобразованием к старому значению j приводит к формуле
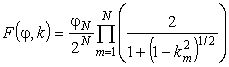 .
.
3.3.2 Вычисление неполного эллиптического интеграла
второго рода E(j, k)
Понижающее
преобразование Ландена является также основой для вычисления одновременно неполных
эллиптических интегралов первого и второго рода. В данном алгоритме
понижающее преобразование Ландена используется совместно с итерационной схемой
АГС. Амплитуда эллиптического интеграла преобразуется по формуле
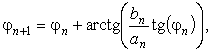
Значения аn, bn вычисляются по схеме АГС, которая
выполняется параллельно. Итерационный процесс должен заканчиваться при
достаточно малом модуле kN , чтобы
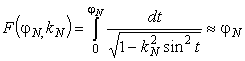 .
.
Возвращение к старому
значению j0 = j приводит к формулам
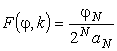 ;
; 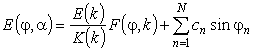 .
.
Эллиптические
функции Якоби могут быть определены через обратную функцию эллиптического
интеграла первого рода. Пусть в интеграле
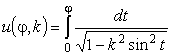
u и j являются комплексными
переменными. Рассмотрим обратную к u функцию
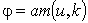 ,
,
называемую амплитудой.
Тогда эллиптическими функциями Якоби являются
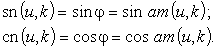
Они называются
соответственно эллиптическим синусом, эллиптическим косинусом.
Функции – мероморфные,
двоякопериодические во всей плоскости комплексного переменного. Отношение их
периодов не является действительным числом. В элементарном (основном) параллелограмме, построенном на наименьших
периодах как на векторах, эллиптические функции Якоби имеют по два
изолированных полюса и нуля.
Вычислять эллиптические
функции Якоби можно с помощью метода АГС.
1.
Исходная
тройка чисел и итерационная схема совпадают
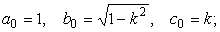
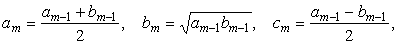
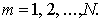
Процесс заканчивается на
таком N, при котором сN » 0 с заданной точностью.
2.
Находим
амплитуду
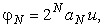
где u - аргумент (вещественный) искомой функции.
3.
Строим
обратную рекуррентную схему:
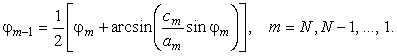
4.
Искомые
функции вычисляются по формулам
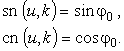
4.Пакет прикладных программ Elastic
Rod
Данный
пакет прикладных программ предназначен для визуализации возможных конфигураций
упругого стержня при различных видах закрепления.
Программа
разработана с использованием современных языков программирования Java, JavaScript и является Интернет приложением. В технологическом смысле это открытая
сетевая разработка, что позволяет любому пользователю сети Интернет не только
управлять программой, но и изменять ее функции.
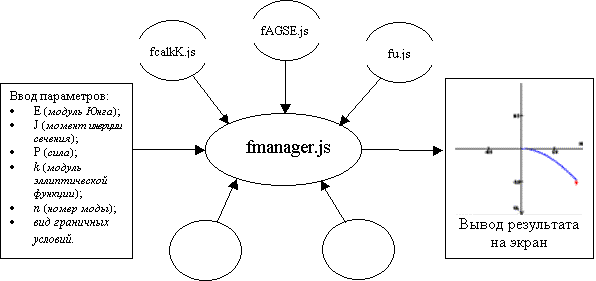
Программа
состоит из набора модулей предназначенных для вычисления эллиптических
интегралов, эллиптический функций, интерфейса ввода вывода и организующего
модуля (fmanager.js), который связывает между
собой модули интерфейсной и функциональной части (Рис. 7). Исходный код и
назначение модулей приведены в приложении 1.
Рис. 7
Открытая
архитектура программы позволяет вносить дополнения касающиеся других видов
закрепления через подключение дополнительного модуля.
Заключение.
В результате работы были рассмотрены точные решения
прогибов упругого стержня для следующих видов закрепления:
·
Консоль
защемленный конец. Поперечное приложение силы.
·
Консоль
защемленный конец. Продольное приложение силы.
·
Консоль
защемленный конец. Произвольное приложение силы.
·
Защемленные
концы. Продольное приложение силы.
·
Закрепленные
концы. Продольное приложение силы.
На основе этих решений
создан программный продукт, позволяющий визуализировать, возможные прогибы
стержня при перечисленных граничных условиях, в зависимости от физических
характеристик стержня, приложенной силы
и моды решения.
Эта программа позволяет
систематизировать задачи об изгибе упругих стержней, что позволяет в едином
ключе решать различные инженерные задачи.
![]() (1)
(1)![]()
![]() (2)
(2)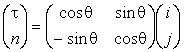 ,
, 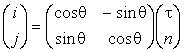 .
.![]() ,
,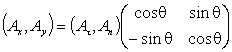 ,
, 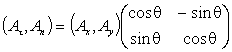 . (3)
. (3)![]() ,
, ![]() . (4)
. (4)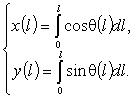 (5)
(5)![]() . (6)
. (6)![]() . (7)
. (7)![]() . (8)
. (8)![]() . (9)
. (9)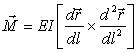
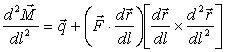 .
.
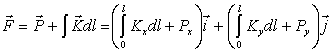 ,
,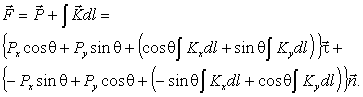



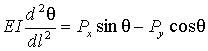 .
.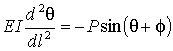 ,
,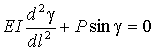 .
.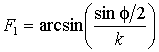
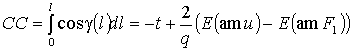


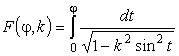 .
.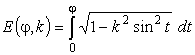 .
.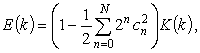
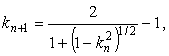
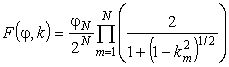 .
.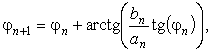
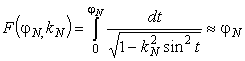 .
.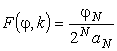 ;
;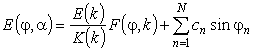 .
.