Содержание
2. Связь между дифференциалами в декартовой и криволинейной системах координат
3. Элемент поверхности. Замена переменных
4. Исследование поверхности с помощью аппарата квадратичных форм
А. Первая квадратичная форма I
Б. Вторая квадратичная форма II
В. Исследование кривизны поверхности
6. Метрический тензор в теории поверхностей
Список литературы
Введение
Наблюдая длительный период развития математики, можно заметить, что диалектически происходит периодическая смена двух основных взглядов на восприятие и описание закономерностей окружающей действительности. В одни эпохи идет алгебраизация с ее формализацией и логическим структурированием языка, торжествуют аксиоматические подходы, иногда в ущерб наглядности и даже возможным приложениям. В другие эпохи главенствует геометризация с ее стремлением к интуитивной наглядности, визуализации, к «картинкам», иногда в ущерб даже формальной строгости доказательств. Психологи утверждают, что и индивидуумы делятся на «левополушарных» и «правополушарных», одни из них тяготеют к счету, к абстракции, другие - к наглядности, к геометрии, к моделям.
Сейчас, как нам кажется, имеется тенденция к очередной геометризации, модельности и, следовательно, к воспитанию навыков образного мышления. Мы обращали уже внимание в наших методических указаниях [5] на то, что эта задача становится особенно актуальной в связи с возрастающим количеством нелинейных задач,возникающих в современной физике и технике, решения которых приводят к сложным визуализациям результатов численных расчетов и экспериментов. Мыслительные процессы человека, такие как инженерное проектирование, научно-теоретическое изучение явлений и их связей, оперируют образами, визуальными формами.
Обучение методам образного мышления является большой и серьезной задачей. В данном пособии делается очередной шаг в этом направлении. Учебников и монографий по геометрии много, и неисчислимо много всевозможных методических пособий по тем или иным частным вопросам. Чем же предлагаемые вниманию читателя методические указания отличаются от остальных?
Один из соавторов из личных пристрастий время от времени вкрапляет в читаемый им на физическом факультете курс математического анализа элементы дифференциальной геометрии; другой соавтор в свое время, будучи студентом, активно воспринял эти «вкрапления»; третий, которому удалось продвинуть недавно некоторые трудные вопросы нелинейной физики, поставил второму задачу о большом изгибе мембраны, которую они решали, опираясь на аппарат дифференциальной геометрии, а результат этой работы вышел, по сути, за рамки классической теории. Сама работа получила медаль Российской академии наук на конкурсе научных работ студентов вузов за 1998 год.
Таким образом, дифференциальная геометрия является типичным рабочим инструментом в некоторых актуальных областях современной нелинейной физики и механики. Мы надеемся, что это пособие будет помогать в работе физикам и механикам, как инженерам, так и теоретикам.
Эта работа подготовлена аспирантом (К.Г. Охоткиным) и преподавателями (В.А. Степаненко и Ю.В. Захаровым) и является одним из результатов сотрудничества в рамках Межвузовского инженерно-физического отделения.
Мы благодарны всем, помогавшим изданию работы.
Любой однозначной функции двух переменных w = f(x, y) можно поставить во взаимнооднозначное соответствие поверхность (ее график), погруженную в обычное евклидово пространство R3, с декартовыми координатами x, y, w. Соответственно в цилиндрических координатах r, φ, w поверхность будет описываться функцией w = f(r, φ) (рис. 1). Такой способ задания поверхности называют явным.
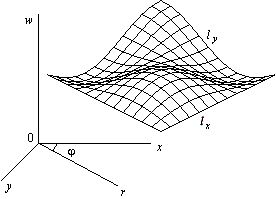
Рис. 1. График поверхности в декартовых координатах
На поверхности можно вводить криволинейную сетку поверхностных координат. Например, lx, ly – поверхностные криволинейные координаты, которые получаются в результате сечения поверхности семейством вертикальных плоскостей wox и woy (рис. 1). Соответственно в цилиндрических координатах можно ввести криволинейные координаты lr, lφ, где lr – криволинейный радиус, получаемый с помощью сечения поверхности плоскостью wor, а lφ = rφ – дуга окружности. Задаваемые таким образом на поверхности криволинейные координаты являются в общем случае косоугольными (углы между координатными линиями на поверхности не всегда прямые, как в случае ортогональных координат).
2. Связь между дифференциалами в декартовой и криволинейной системах координат
Введем угол наклона касательной θx к кривой, получаемой сечением поверхности w = f(x, y) вертикальной плоскостью wox, в текущей точке x (рис. 2). Аналогично вводятся углы θy и θr для цилиндрической системы координат.
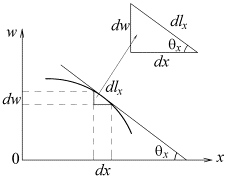
Рис. 2. Сечение wox поверхности w = f(x, y)
Напишем основные выражения, связывающие дифференциалы в декартовой системе координат dx, dy и в криволинейной системе координат dlx, dly. Имеем в сечениях wox(рис. 2)
для сечений woy: ![]() ,
, ![]() ,
, 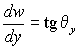 .
.
Соответствующие формулы верныив цилиндрических координатах для сечения wor. Можно также сказать, что формулы (2) задают неявно связь между декартовыми переменными и криволинейными длинами на поверхности, в общем случае x(lx, ly), y(lx, ly), z(lx, ly, θx, θy).
3. Элемент поверхности. Замена переменных
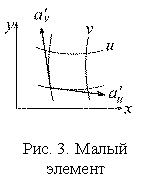
А. Изменение при переходе из одной системы координат (x, y) в другую (u, v) элемента площади dS0 в двумерном случае
Рассмотрим малый элемент площади dS0 в плоскости (x, y) (рис. 3).
Введем радиус-вектор
![]() .
.
Его дифференциал в произвольном направлении l
![]() .
.
Площадь малого элемента dS0 построим как модуль векторного произведения двух векторов:
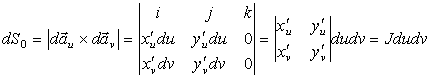 ,
,
где J – определитель матрицы якобиана перехода. Т.е. dS0 = dxdy = Jdudv. В современной дифференциальной геометрии переход осуществляется введением дифференциальной формы ω = dS0 = dx ^ dy = Jdu ^ dv, где ^ - внешнее произведение. (См., например, [1], [2]). Приведем пример для полярной системы координат:
dS0 = rdrdφ, J = r.
Б. Замена системы координат для элементарной площадки на поверхности
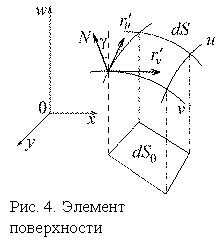 Необходимость выражения дифференциала
площади элемента поверхности в различных криволинейных координатах возникает,
прежде всего, в процессе вычисления поверхностных интегралов, при переходе к
двойному интегралу. Введем обозначения: dS
– поверхностный элемент площади (рис. 4), dS0 – площадь
элемента, лежащего в плоскости xoy, или проекция на эту плоскость dS, т.е. dS0 = dScosγ,
где
Необходимость выражения дифференциала
площади элемента поверхности в различных криволинейных координатах возникает,
прежде всего, в процессе вычисления поверхностных интегралов, при переходе к
двойному интегралу. Введем обозначения: dS
– поверхностный элемент площади (рис. 4), dS0 – площадь
элемента, лежащего в плоскости xoy, или проекция на эту плоскость dS, т.е. dS0 = dScosγ,
где ![]() ,
, ![]() – вектор нормали.
Криволинейные ортогональные координаты на поверхности - u, v. Поверхность задана явно, w = f(x, y).
Радиус-вектор текущей точки -
– вектор нормали.
Криволинейные ортогональные координаты на поверхности - u, v. Поверхность задана явно, w = f(x, y).
Радиус-вектор текущей точки - ![]() имеет компоненты:
имеет компоненты:
x = x(u, v), y = y(u, v), w = w(x(u, v), y(u, v)).
Это задание поверхности в параметрической форме. Построим математическую модель площади с помощью векторного произведения дифференциалов радиус-вектора, аналогично пункту А:
Выражение ![]() называется
детерминантом первой квадратичной формы, см. следующий пункт, (6). В частном
случае, когда в качестве криволинейных координат выбираются собственно
декартовые координаты, имеем
называется
детерминантом первой квадратичной формы, см. следующий пункт, (6). В частном
случае, когда в качестве криволинейных координат выбираются собственно
декартовые координаты, имеем
w = f(x, y),
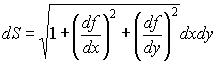 .
.
Пример: элемент площади в цилиндрических координатах и при осевой симметрии,
когда w = f(r) и d/ dφ = 0, имеет вид:
4. Исследование поверхности с помощью аппарата квадратичных форм
А. Первая квадратичная форма I
Определение
В каждой точке поверхности можно ввести квадратичную форму
где (ξ, η) – криволинейные поверхностные координаты.
Общеприняты следующие обозначения для коэффициентов формы:
a11 = E, a12 = F, a22 = G. (6)
Поясним геометрический смысл первой формы. Пусть ![]() – радиус-вектор. Его
дифференциал
– радиус-вектор. Его
дифференциал
и тогда
где dl – элемент дуги поверхности в произвольном направлении l. Таким образом, первая квадратичная форма определяет квадрат dl. Определим коэффициенты формы, подставив (7) в (8):
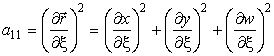 ,
,
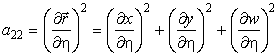 .
.
Если χ - угол между касательными
векторами (между координатными линиями на поверхности в текущей точке), то ![]() . Для ортогональных координат на поверхности χ =
π/2, a12 = 0.
. Для ортогональных координат на поверхности χ =
π/2, a12 = 0.
Введем обозначение для детерминанта квадратичной формы
Рассмотрим рис. 5. В текущей точке M построим касательные векторы ![]() и
и ![]() . Плоскость L,
проведенная через них, является касательной плоскостью к поверхности в точке М. Линия, перпендикулярная к плоскости и
проведенная через точку М, является
нормалью в текущей точке к поверхности. Ее направление определяется векторным
произведением касательных векторов. Единичный вектор нормали находим из
следующего выражения:
. Плоскость L,
проведенная через них, является касательной плоскостью к поверхности в точке М. Линия, перпендикулярная к плоскости и
проведенная через точку М, является
нормалью в текущей точке к поверхности. Ее направление определяется векторным
произведением касательных векторов. Единичный вектор нормали находим из
следующего выражения:
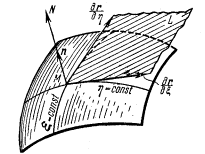
Рис. 5. Координатные векторы в точке М
Таким образом, первая квадратичная форма описывает поверхность в первом приближении, когда малый участок поверхности заменяется на участок касательной плоскости. Первая квадратичная форма определяет углы между линиями и длины дуг на поверхности, а также площади любых участков поверхности (см. (3)). Малый элемент площади поверхности
где ![]() -
криволинейные дифференциалы на поверхности, получаемые по формулам типа (1), (2).
-
криволинейные дифференциалы на поверхности, получаемые по формулам типа (1), (2).
Б. Вторая квадратичная форма II
Вторая квадратичная форма описывает поверхность во втором приближении. Она показывает, как отклоняется поверхность от касательной плоскости, и полностью определяет кривизну поверхности.
Определение
Коэффициенты формы определяются следующими выражениями:
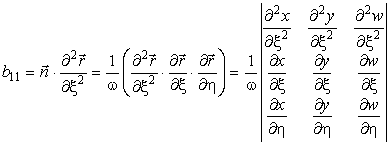 ,
,
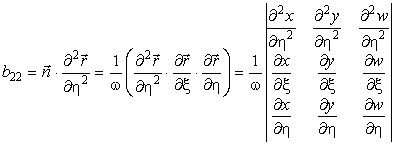 .
.
В. Исследование кривизны поверхности
Определение
Для двумерного случая скалярной кривизной кривой, лежащей в плоскости, называется величина
взятая в текущей точке кривой.
Здесь все векторы лежат в одной плоскости. В литературе часто встречаются определения кривизны (15) с разными знаками, которые можно трактовать различно, в зависимости от конкретной задачи. Общий физический смысл: кривизна кривой линии пропорциональна моменту сил, изгибающих ее.
Для пространственного случая нормальной кривизной линии l, получаемой нормальным сечением поверхности, называется величина
взятая в текущей точке линии. Если вертикальное и
нормальное сечения совпадают, то совпадают и величины кривизн (15) и (16).
Кривизна κ в произвольном наклонном сечении определяется из (16) по
теореме Менье: ![]() , где γ – угол между этим наклонным и нормальным
сечениями.
, где γ – угол между этим наклонным и нормальным
сечениями.
Выберем в качестве параметра, определяющего положение точки на кривой, длину дуги. Тогда криволинейные координаты точки будут функциями длины дуги l: ξ(l), η(l). Выражение (7) перейдет в
Векторы ![]() и
и ![]() перпендикулярны нормали
перпендикулярны нормали
![]() , (см. рис. 5). Имеем из (16)
, (см. рис. 5). Имеем из (16)
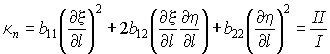 ,
,
Найдем из (18) нормальные кривизны координатных линий:
1) η = Const, dη = 0, ![]() ;
;
Параметр b12/w определяет кручение поверхности. Проследим за изменением κn при повороте сечения вокруг нормали к поверхности. Для гладких поверхностей кривизна будет плавно периодически изменяться от минимального до максимального значения. Найдем их. Перепишем выражение (18) в виде
![]() .
.
Раскрывая скобки и перегруппировывая члены выражения, имеем
![]() .
.
Получили квадратичную форму
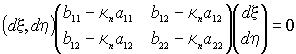 .
.
Необходимым и достаточным условием существования нетривиального решения по теореме Крамера является равенство нулю определителя этой матрицы. Имеем квадратное уравнение для кривизны
![]() .
.
Отсюда находим два экстремальных значения κn, которые называются главными кривизнами поверхности в данной точке. Соответствующие им направления (для отношения dξ:dη) называются главными. Главные направления взаимно перпендикулярны.
Проведем линии на поверхности таким образом, чтобы в каждой точке касательные к ним шли вдоль главных направлений. Такие кривые называются линиями кривизны; их удобно выбирать в качестве координатных кривых. Если поверхностная координатная сеть (ξ, η) совпадает с линиями кривизны поверхности, то главные кривизны совпадают с (19). Если коэффициент первой формы a12 = 0, то это сеть ортогональных криволинейных координат (для них c = p/2); если b12 = 0, то сеть называется сопряженной.
По свойству решений квадратного уравнения имеем для произведения и полусуммы главных кривизн выражения
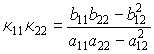 ,
, 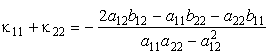 .
.
Определение
Гауссовой кривизной поверхности в данной точке называется величина
Средней кривизной поверхности в данной точке называется величина
Пусть дана обычная (лабораторная) система координат x (x1, x2, …, xn). Сделаем переход в произвольную криволинейную (не обязательно ортогональную) систему координат y (y1, y2, …, yn). Радиус-вектор и матрица Якоби будет задаваться следующим образом (здесь пишем верхние индексы – используем контравариантные координаты):
В этой матрице столбцы являются компонентами
касательных векторов ![]() к координатным линиям
y1, y2, …, yn.
Если их нормировать, то получим набор базисных векторов
к координатным линиям
y1, y2, …, yn.
Если их нормировать, то получим набор базисных векторов ![]() в пространстве x.
в пространстве x.
Определение
Метрический тензор в базисе ![]() имеет вид
имеет вид
Символы Кристоффеля (коэффициенты связности)
Введем тензорные обозначения касательных векторов и их производных:
![]()
![]() ,
, ![]() .
.
Векторы производных разложим по базисным векторам:
где коэффициенты разложения ![]() - некоторые функции координат, вид которых
зависит от выбора системы координат; в декартовой системе все
- некоторые функции координат, вид которых
зависит от выбора системы координат; в декартовой системе все ![]() . Отсюда видно, что величины
. Отсюда видно, что величины ![]() не образуют тензора,
так как тензор, равный нулю в одной системе координат, равен нулю и во всякой
другой. В данной метрике символы Кристоффеля вычисляются по формулам
не образуют тензора,
так как тензор, равный нулю в одной системе координат, равен нулю и во всякой
другой. В данной метрике символы Кристоффеля вычисляются по формулам
доказательство которых приведем ниже.
Ковариантная производная
Найдем, как преобразуется производная от произвольной вектор-функции ∂Ai/ ∂yj при переходе от декартовых к криволинейным координатам. Для того чтобы получить дифференциал вектора, необходимо, чтобы оба вектора находились в одной точке пространства. Но в криволинейных координатах разность компонент векторов после параллельного переноса их в одну точку не совпадает с их разностью до переноса (т.е. с дифференциалом dAi). Изменение компонент вектора при бесконечно малом параллельном переносе зависит линейно от самих компонент. Таким образом, запишем точные производные в криволинейных координатах, так называемые ковариантные производные (которые являются тензорами)
соответственно от контравариантного и ковариантного векторов и тензора. В декартовой метрике они, очевидно, совпадают с обычными производными.
Определение
Линия пространства yi = yi(t) называется геодезической, если ее вектор скорости Ai = dyi / dt параллелен вдоль нее самой, т.е. его ковариантная производная равна нулю.
Уравнение геодезических линий
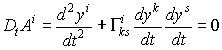 .
.
Если все символы Кристоффеля равны нулю, то решениями этого уравнения являются обычные прямые. Таким образом, геодезические линии являются аналогом прямых для случая произвольной кривизны пространства.
Тензор кривизны Римана
Если дважды ковариантно продифференцировать вектор Ai, то результат зависит, вообще говоря, от порядка дифференцирования, в противоположность от обычных производных. Запишем эту разность
![]() ,
,
где
![]() - тензор 4-го ранга:
- тензор 4-го ранга:
Этот тензор называется тензором кривизны Римана данной метрики. Свойства тензора для симметричных связностей:
![]() ,
, ![]() .
.
Из тензора Римана можно путем упрощения построить тензор второго ранга - тензор Риччи, являющийся следом тензора Римана
Свернув метрикой тензор Риччи, получим инвариант - след тензора Риччи
называемый скалярной кривизной данного пространства. Гауссова кривизна, определенная в (19), связана со скалярной следующим образом: 2K = R.
Тензором кручения пространства называется выражение
Если связность ![]() является
симметричной, то тензор кручения равен нулю. Поясним геометрический смысл
тензора кручения на рис. 6. Рассмотрим поверхность S. В точке А к S построим касательную
плоскость p. Выберем произвольный
бесконечно малый квадрат ABCD
на плоскости p с вершиной в А. Из точки А по поверхности S
выпустим геодезическую в направлении вектора AB. Пройдя по ней расстояние,
соответствующее параметру, равному длине AB, попадем в точку B'. Аналогично из А по S выпустим геодезическую в направлении AD, попадем в D'.
Совершим параллельный перенос вектора AD в точку B'
вдоль геодезической AB' и выпустим геодезическую из
B'
вдоль перенесенного вектора, попадем в точку С'. Аналогично вектор AB перенесем параллельно вдоль
AD' и
вдоль перенесенного вектора из D' выпустим геодезическую,
попадем в C''.
Если кручение нулевое, то C' = C'',
и геодезический квадрат с точностью до малых более высокого порядка замкнется,
в противном случае нет.
является
симметричной, то тензор кручения равен нулю. Поясним геометрический смысл
тензора кручения на рис. 6. Рассмотрим поверхность S. В точке А к S построим касательную
плоскость p. Выберем произвольный
бесконечно малый квадрат ABCD
на плоскости p с вершиной в А. Из точки А по поверхности S
выпустим геодезическую в направлении вектора AB. Пройдя по ней расстояние,
соответствующее параметру, равному длине AB, попадем в точку B'. Аналогично из А по S выпустим геодезическую в направлении AD, попадем в D'.
Совершим параллельный перенос вектора AD в точку B'
вдоль геодезической AB' и выпустим геодезическую из
B'
вдоль перенесенного вектора, попадем в точку С'. Аналогично вектор AB перенесем параллельно вдоль
AD' и
вдоль перенесенного вектора из D' выпустим геодезическую,
попадем в C''.
Если кручение нулевое, то C' = C'',
и геодезический квадрат с точностью до малых более высокого порядка замкнется,
в противном случае нет.

Скалярным произведением двух произвольных векторов
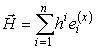 ,
, 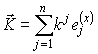
в метрике gij будет следующая билинейная форма:
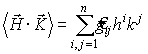 .
.
Для частного случая евклидова пространства
метрический тензор ![]() - единичная матрица, и скалярное произведение
принимает обычный вид
- единичная матрица, и скалярное произведение
принимает обычный вид
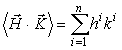 .
.
Если взять скалярное произведение двух одинаковых векторов, то получим положительно определенную квадратичную форму
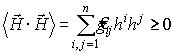 ,
,
следовательно, detg> 0.
Дивергенция вектора имеет вид
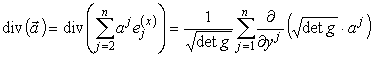 .
.
Градиент функции f имеет вид
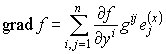 .
.
Оператор Лапласа в произвольных криволинейных координатах:
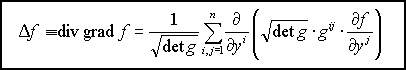 |
В ортогональных криволинейных координатах матрица метрического тензора имеет диагональный вид
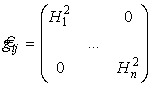 ,
,
где положительные функции Hi- коэффициенты Ламе системы координат и ![]() . Они соответствуют корням из коэффициентов первой
квадратичной формы a11 и a22 в теории поверхностей.
. Они соответствуют корням из коэффициентов первой
квадратичной формы a11 и a22 в теории поверхностей.
Пример 1
Оператор Лапласа в евклидовом пространстве R3, в декартовых координатах.
Здесь n= 3, x1 = x, x2 = y, x3 = z. Лапласиан принимает вид
Пример 2
Оператор Лапласа в евклидовом пространстве R3, в сферических координатах:
x1 = rsinθcosφ, x2 = rsinθcosφ, x3 = rcosθ, (здесь n= 3, y1 = r, y2 = θ, y3 = φ).
Ортонормированный базис er, eq, ej, ![]() . Лапласиан принимает вид
. Лапласиан принимает вид
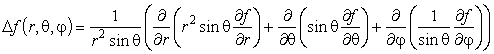 .
.
Пример 3
Оператор Лапласа в евклидовом пространстве R3, в цилиндрических координатах:
x1 = r cos φ, x2 = r sinφ, x3 = z. (здесь n = 3, y1 = r, y2 = φ, y3 = z). Лапласиан принимает вид
6. Метрический тензор в теории поверхностей
А. Метрика поверхности
Рассмотрим поверхность w = w(x, y) в евклидовом пространстве R3. Применим для исследования этой поверхности приведенный выше тензорный аппарат дифференциальной геометрии. Будем задавать поверхность в параметрическом виде как геометрическое место точек, описываемых радиус-вектором, проведенным из начала координат (так же, как и при рассмотрении первой квадратичной формы поверхности):
![]() ,
,
поверхностные криволинейные координаты
y1 = ξ, y2 = η, n = 2.
Введем тензорные обозначения для производных радиус-вектора поверхности по криволинейным координатам:
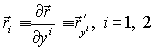 ;
; 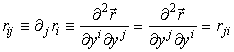 .
.
Получим метрический тензор поверхности так же, как и в (23):
его компоненты образуют матрицу, совпадающую с матрицей первой квадратичной формы поверхности
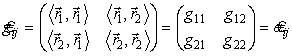 ,
,
т.е. gij = aij, и в тензорных обозначениях первая квадратичная форма примет следующий вид:
I = dl2 = dr2 = gij dyidyj, gij = gji.
Детерминант матрицы
![]() .
.
Ковариантные компоненты метрического тензора находим, обращая матрицу
С помощью метрического тензора выполняют операции поднятия и опускания индексов, например, для нахождения ковариантных компонент векторов:
![]() .
.
Б. Единичный орт нормали в текущей точке поверхности (см. (11)
![]() .
.
В. Элементарный элемент площади на поверхности
Угол
между касательными векторами ![]() ,
, ![]() .
.
Элемент площади (см. (12)
Г. Вторая квадратичная форма записывается в тензорных обозначениях как
II = bij dyidyj, ее коэффициенты вычисляются по формулам
Они подчинены двум уравнениям Петерсона-Кодацци
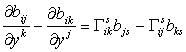 , i, j, k
= 1, 2.
, i, j, k
= 1, 2.
Д. Криволинейный оператор Лапласа записывается так же, как и в (32):
Е. Локальный базис и символы Кристоффеля поверхности
В текущей точке y1, y2 поверхности касательные векторы r1, r2 и орт нормали n образуют сопутствующий локальный базис (триэдр) в R3, причем
Разложим вектор второй производной в локальном базисе
и найдем неизвестные коэффициенты разложения ![]() и
и ![]() . Для этого умножим скалярно обе части уравнения (41) сначала
на вектор нормали n:
. Для этого умножим скалярно обе части уравнения (41) сначала
на вектор нормали n:
![]() .
.
Так как касательные векторы и орт нормали перпендикулярны, то имеем
![]() .
.
Этот коэффициент действительно совпадает с коэффициентами
второй квадратичной формы (38). Умножим теперь обе части уравнения на
касательный вектор ![]() :
:
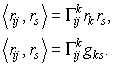
Выразим коэффициенты ![]() явно, для этого
умножим обе части уравнения на ковариантный метрический тензор
явно, для этого
умножим обе части уравнения на ковариантный метрический тензор
Скалярное произведение, стоящее в левой части уравнения,
можно выразить через компоненты метрики. Продифференцируем метрику ![]() по координате и
проведем циклические перестановки индексов:
по координате и
проведем циклические перестановки индексов:
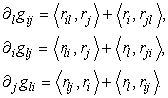
Сложим последние два уравнения и вычтем первое:
![]() ,
,
окончательно имеем известное выражение
![]() (43)
(43)
для коэффициентов, которые называются символами Кристоффеля 2 рода. Таким образом, мы получили два уравнения (42) и (43) для нахождения коэффициентов Кристоффеля и уравнение (41) для проверки. Тензор кривизны Римана поверхности определяется так же, как и в (27).
Пример 1
Рассмотрим заданную явно поверхность w = w(x, y) в декартовых координатах:
y1 = ξ = x, y2 = η = y.
Имеем радиус-вектор точки поверхности
![]() .
.
Первые и вторые производные радиус-вектора
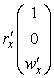 ,
, 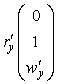 ,
, 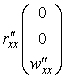 ,
,  ,
, 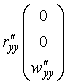 .
.
Метрика (матрица первой квадратичной формы) по определению (35)
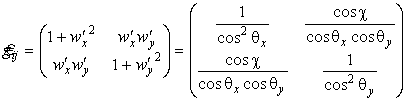 ,
,
![]() .
.
Единичный вектор нормали имеет вид
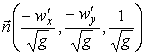 .
.
Малый элемент площади поверхности, с использованием соотношений (2)
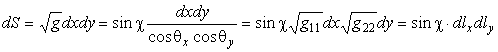 .
.
Криволинейный оператор Лапласа в общем косоугольном случае
в частном случае поверхности, на которой возникли
ортогональные криволинейные координаты (![]() ), имеем
), имеем
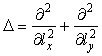 .
.
Матрица второй квадратичной формы
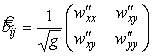 .
.
Главные кривизны найдем по формулам (19):
Для осесимметричной поверхности логично перейти в полярные координаты. Если здесь сделать формальную замену переменных (49), то получим формулы для кривизн в полярных координатах (50).
В выражениях (45) корень, стоящий в знаменателе, является модулем вектора нормали к поверхности в текущей точке. Если для этой поверхности нормальное сечение совпадает с вертикальным, то кривизны (45) перейдут в
В частном случае малых прогибов поверхности (углов наклона касательной) в выражениях (46) можно пренебречь квадратом производной по сравнению с единицей и получить выражения для малых кривизн (геометрически линейный случай):
Символы Кристоффеля можно найти по формуле (43) или по формуле (42):
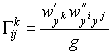 .
.
По формулам (27) вычислим компоненты тензора кривизны Римана
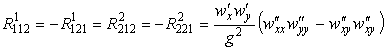 ,
,
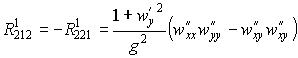 ,
, 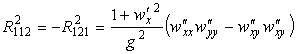 .
.
Остальные компоненты равны нулю. Найдем тензор Риччи по формуле (29)
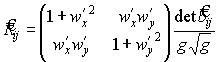 .
.
Скалярная кривизна по формуле (30)
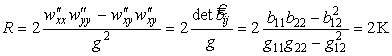 ,
,
где К - гауссова кривизна, см. формулу (20).
Пример 2
Рассмотрим осесимметричную
поверхность, заданную явно функцией w(r), в цилиндрических координатах. Для
этого случая пропадает зависимость от полярного угла φ, и все ![]() , поэтому частные производные по полярному радиусу совпадают
с полными производными.
, поэтому частные производные по полярному радиусу совпадают
с полными производными.
Координаты y1 = ξ = r, y2 = η = φ. Используя формулы замены переменных, запишем радиус-вектор
![]() .
.
Выпишем производные от радиус-вектора по координатам
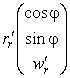 ,
, 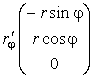 ,
, 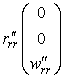 ,
, 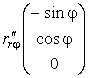 ,
, 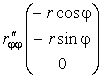 .
.
Компоненты метрического тензора (коэффициенты первой квадратичной формы) найдем по формулам (35) или (9):
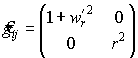 ,
, 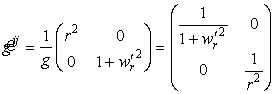 ,
, ![]() .
.
Отсюда видно, что мы получили на поверхности сетку ортогональных криволинейных координат. Оператор Лапласа
Для случая пологих поверхностей, когда можно пренебречь
квадратом производной ![]() по сравнению с
единицей, оператор (48) совпадает с обычным оператором Лапласа в полярных
координатах (см., например, (34). Выражение (48) можно получить из (44)
прямой заменой декартовых координат на полярные для осесимметричного случая.
Приведем эти формулы перехода
по сравнению с
единицей, оператор (48) совпадает с обычным оператором Лапласа в полярных
координатах (см., например, (34). Выражение (48) можно получить из (44)
прямой заменой декартовых координат на полярные для осесимметричного случая.
Приведем эти формулы перехода
Коэффициенты второй квадратичной формы
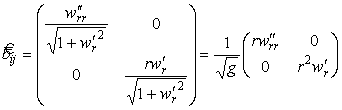 .
.
Главные кривизны поверхности найдем по формулам (19):
Здесь ![]() , т.е. использована замена переменных w(r) на θ(r),
вида (2).
Выражения (50) можно получить заменой переменных (49) непосредственно из
приведенных выше кривизн (45) в декартовой системе координат.
, т.е. использована замена переменных w(r) на θ(r),
вида (2).
Выражения (50) можно получить заменой переменных (49) непосредственно из
приведенных выше кривизн (45) в декартовой системе координат.
Кручение поверхности отсутствует в осесимметричном случае, так как диагональный коэффициент второй квадратичной формы b12 = 0. Из (50) видны свойства главных кривизн:
Символы Кристоффеля
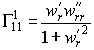 ,
, 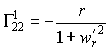 ,
, ![]() ,
, ![]() .
.
Отличные от нуля компоненты тензора Римана
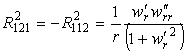 ,
, 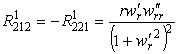 .
.
Скалярную кривизну поверхности найдем, дважды свернув тензор Римана
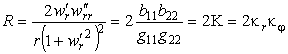 .
.
Вычислим для примера главные
кривизны псевдосферы - поверхности, образованной
вращением трактрисы ![]() относительно оси Ow (трактриса является эвольвентой
цепной линии
относительно оси Ow (трактриса является эвольвентой
цепной линии ![]() ). Используя
формулы (50),
найдем кривизны
). Используя
формулы (50),
найдем кривизны
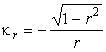 ,
, 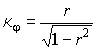 .
.
Гауссова кривизна ![]() постоянна и
отрицательна на всей поверхности. Выполняя интегрирование
постоянна и
отрицательна на всей поверхности. Выполняя интегрирование
![]() ,
,
получим длину дуги вдоль радиуса на поверхности псевдосферы.
Список литературы
1. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. – М.: Наука, 1985.
2. Новиков С.П., Фоменко А.Т. Элементы дифференциальной геометрии и топологии. – М.: Наука, 1987.
3. Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: Наука, 1988.
4. Ландау Л.Д., Лифшиц Е.М. Теория упругости. - М.: Наука, 1987.
5. Поверхности функций комплексного переменного: Метод. указания, ч. 5 / Краснояр. гос. ун-т; Сост. Ю.В. Захаров, К.Г. Охоткин, Л.С. Титов. Красноярск, 1996.
6. Победря Б.Е. Лекции по тензорному анализу. - М.: Изд-во МГУ, 1986.
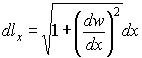 , (1)
, (1)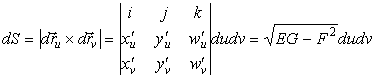
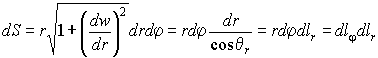
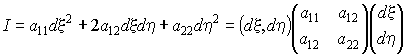
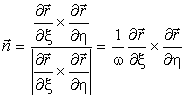
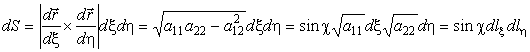
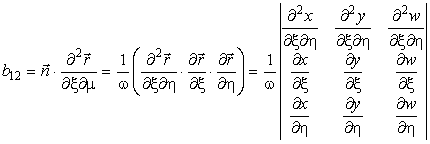
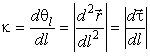
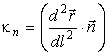
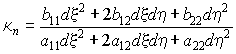
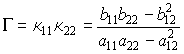
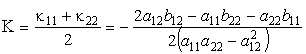
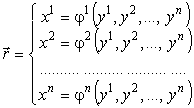
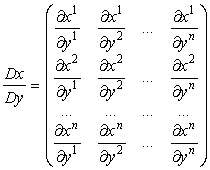 . (22)
. (22)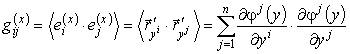
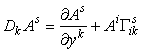
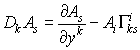 ,
, 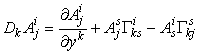 , (26
, (26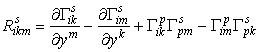
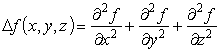
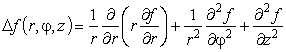
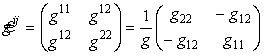
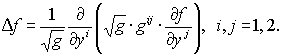 (
(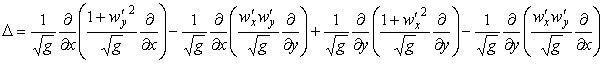
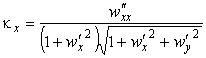
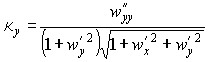
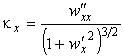
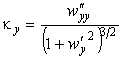
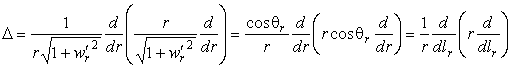
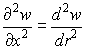 ,
, 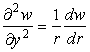 ,
, 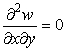 . (
. (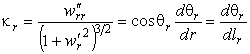
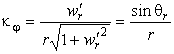 . (5
. (5