МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ

имени академика М.Ф. Решетнева

Кафедра технической физики

 

Лабораторная работа №6

БЕСКОНТАКТНЫЙ МЕТОД ИЗМЕРЕНИЯ УДЕЛЬНОГО ЭЛЕКТРОСОПРОТИВЛЕНИЯ ПОЛУПРОВОДНИКОВЫХ ПЛАСТИН И ТОНКИХ МЕТАЛЛИЧЕСКИХ ПЛЕНОК

 

Методические указания к выполнению лабораторной работы по курсу «Твердотельная электроника»

 

Составитель: Паршин А.С.

 

Красноярск 2003

 

Лабораторная работа №6. Бесконтактный метод измерения удельного электросопротивления полупроводниковых пластин и тонких металлических пленок

 

Цель работы: Экспериментальное определение удельного электросопротивления и концентрации носителей заряда полупроводниковых пластин и тонких пленок металлов.

 

1. Электропроводность металлов

 

Простейшей моделью электропроводности металлов является модель свободных электронов. Согласно этой модели валентные электроны, как наиболее слабо связанные с атомами, составляющих металл, могут свободно перемещаться в объеме кристаллической решетки. Они являются носителями электрического тока в металле, и их часто называют электронами проводимости. В этой модели можно пренебречь силами взаимодействия между электронами проводимости и ионными основами, полную энергию электронов проводимости можно считать равной их кинетической энергии, а потенциальной энергией можно пренебречь.

Классическая теория электропроводности была развита задолго до создания квантовой механики и имела ряд выдающихся успехов, к которым в первую очередь следует отнести выводы закона Ома и соотношения между электропроводностью и теплопроводностью металлов (закон Видемана-Франца). Ограниченность этой теории проявилась в неспособности объяснить температурной зависимости теплоемкости и парамагнитной восприимчивости электронов проводимости. Другим важным недостатком этой теории явилось расхождение между теоретическими оценками длины свободного пробега и экспериментальных измерениях этой величины. В наиболее чистых образцах при низких температурах средняя длина свободного пробега может достигать 10⁸-10⁹ межатомных расстояний (более 1 см), что намного превышает ожидаемые классические оценки.

Ответ на вопрос, почему конденсированная среда, какой является кристалл металла, столь прозрачна для электронов проводимости, связан с фундаментальным положением квантовой физики твердого тела–теоремой Блоха. Согласно этой теореме, движение электрона в кристалле можно рассматривать как движение свободной частицы, на которую не действуют ионные основы, но с другой эффективной массой. Однако, если трансляционная симметрия кристаллического поля оказалось нарушенной, например, в результате отклонения некоторого количества ионов от равновесных положений в результате тепловых колебаний, образования вакансий, дислокации и т.д., то условие свободного движения электронов в решетке нарушается. Это приведет к рассеянию электронов на атомах, смещение которых нарушило идеальность структуры кристалла. В связи с этим, электрон в кристалле следует также рассматривать как квазичастицу, имеющую эффективную массу и квазиимпульс. Вне кристалла электрон обладает массой и импульсом свободной частицы.

Основные дефекты, приводящие к рассеянию электронов в кристалле,–это примесные ионизированные атомы и тепловые колебания решетки. При рассеянии на тепловых колебаниях решетки с частотой ω энергия электрона увеличивается или уменьшается на величину, равную энергии фонона . С точки зрения концепции квазичастиц, происходит поглощение фонона электроном или его испускание.

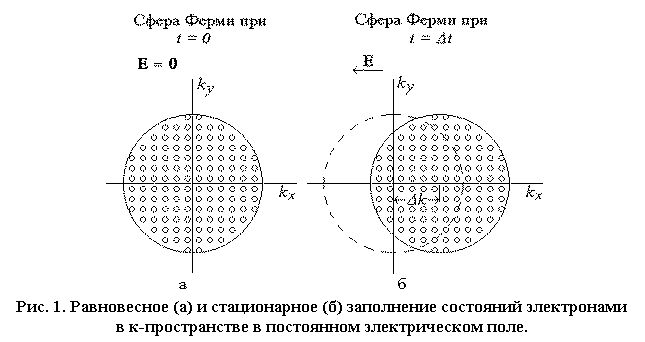
Возникновение электрического тока в металле связано с дрейфом электронов проводимости во внешнем электрическом поле. В зонной теории твердых тел показано, что необходимым условием существования электропроводности у кристаллов является наличие в их энергетической диаграмме частично заполненных электронами энергетических зон. При Т = 0^○К газ электронов в металле полностью заполняет все состояния внутри изоэнергетической поверхности в к–пространстве, соответствующей энергии Ферми (рис. 1а). Такая поверхность в к–пространстве называется поверхностью Ферми. Положение центра сферы Ферми в начале системы координат говорит о том, что направленный перенос заряда в этом состоянии, которое называют равновесным, отсутствует.

Импульс электрона связан с его волновым вектором соотношением

,                                                        (1)

здесь m_n – эффективная масса электрона.

Электрическое поле вызывает ускорение электронов и их переход в новые состояния, лежащие правее исходных, если вектор электрического поля противоположен оси х (рис. 1б).

Уравнение движения электрона под действием электрического поля будет иметь вид

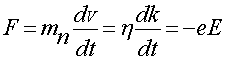                                                 (2)

Под действием постоянной силы F, действующей в течении промежутка времени Δt, каждый электрон, находившийся в состоянии с волновым вектором k, изменит свое состояние так, что его волновой вектор увеличится на . Таким образом, в отсутствие столкновений внешнее постоянное электрическое поле однородно смещает все точки сферы Ферми на величину Δk. Интегрируя уравнение (2), получим:

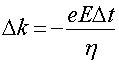                                                                (3)

Процессы рассеяния стремятся вернуть электроны в равновесное состояние. Если внешнее электрическое поле постоянное, то между этими двумя процессами устанавливается динамическое равновесие, наступает, так называемое, стационарное состояние (рис. 1б). Если среднее время между столкновениями равно τ, то стационарное смещение сферы Ферми определяется выражением (3), в котором Δt следует заменить на τ. Параметр τ характеризует время, в течение которого поле действует на электрон, и называется временем релаксации. В стационарном состоянии каждый электрон имеет приращение скорости в одном и том же направлении, противоположном вектору Е. Это дополнительное к хаотическому тепловому движению электронов движение под действием электрического поля называется дрейфом электронов. Величина дрейфовой скорости

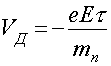                                                                              (4)

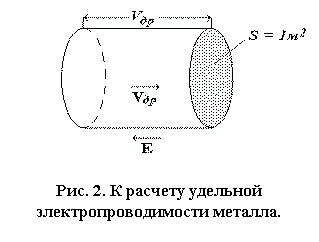Дрейф электронов определяет величину плотности электрического тока в кристалле. Построим мысленно в объеме проводника цилиндр с основанием, равным единице площади, и образующей, равной скорости дрейфа V_Д и направленной вдоль дрейфа (рис. 2). Все электроны, заключенные в этом цилиндре, в течение 1 с пройдут через его основание и образуют ток с плотностью

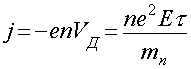                       (5)

здесь n–концентрация электронов проводимости.

Выражение (5) имеет форму закона Ома. Электропроводность есть по определению коэффициент пропорциональности между плотностью тока j и напряженность электрического поля Е, т.е. .Следовательно, из (5) имеем

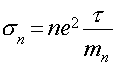                  (6)

Удельное электросопротивление есть по определению величина, обратная удельной электропроводности

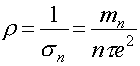                                                           (7)

Подвижностью электронов называют величину, равную отношению скорости дрейфа к напряженности электрического поля

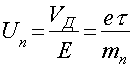                                                             (8)

Иными словами, подвижность–это дрейфовая скорость, приобретенная электронами в электрическом поле единичной напряженности. Оценки скорости дрейфа электронов в кристалле меди в полях напряженности Е=10^–8 В/м дают величину V_Д ~ 0,3 м/с. Это намного порядков ниже скорости движения электронов в отсутствии поля (1,6·10⁶ м/с). Поэтому с приложением поля средняя скорость электронов в проводнике остается практически неизменной.

Подвижность электронов в кристалле определяется механизмами рассеяния электронов проводимости. Как указывалось выше, электросопротивление большинства металлов обусловлено столкновениями электронов с нарушениями регулярной структуры решетки. При комнатной температуре и выше основное значение имеет рассеяние электронов с решеточными фононами (нарушения, связанные с тепловыми колебаниями атомов). При низких температурах электросопротивление обусловлено столкновениями с примесными атомами и механическими дефектами решетки. В связи с этим, удельное сопротивление металла можно записать в виде суммы

                                                                    (9)

где ρ_L–часть удельного сопротивления, обусловленная тепловым движением атомов решетки, ρ_i – часть, обусловленная рассеянием электронов на примесных атомах.

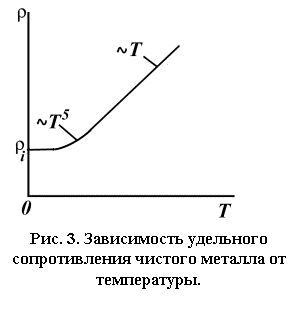Фононный вклад в электросопротивление в простых металлах зависит от температуры по разному: при высоких температурах в основном по закону ρ_L~ Т. При более низких температурах удельное электросопротивление зависит от температуры по степенному закону: ρ_L~.Т⁵. Если концентрация примесных атомов невелика, то часть ρ_i оказывается не зависящей от температуры. На рис. 3. показана схематически температурная зависимость удельного электросопротивления металла. Остаточное сопротивление получается путем экстраполяции кривой к T=0^○К. Эта величина эквивалентна ρ_i, поскольку ρ_L при Т=0^○К обращается в нуль.

 

2. Электропроводность полупроводников

 

Рассуждения, приведенные выше при выводе формулы для электропроводности металла, справедливы как для электронов проводимости, так и для дырок. Для дырочного полупроводника

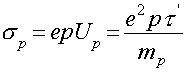                                                           (10)

где p – концентрация дырок; U_p – подвижность дырок; τ^' – время релаксации дырок; m_p – эффективная масса дырки.

В общем случае удельная электропроводность определяется как электронами, так и дырками:

                                          (11)

Электронная составляющая проводимости определяется первым слагаемым в формуле (11), второе слагаемое связано с дырочной проводимостью полупроводника.

Величина удельной проводимости полупроводника и ее температурная зависимость зависят от концентраций носителей (электронов и дырок) и их подвижностей, которые в свою очередь определяются типом полупроводника.

В собственном полупроводнике концентрации электронов и дырок одинаковы (n=p) и последнее равенство принимает вид

                                                      (12)

Электропроводность собственного полупроводника называют собственной электропроводимостью и обозначают обычно .

Концентрация носителей заряда в собственном полупроводнике

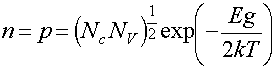                                     (13)

здесь Еg – ширина запрещенной зоны; N_C – эффективная плотность состояний в зоне проводимости; N_V – эффективная плотность состояний в валентной зоне,

 

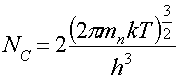
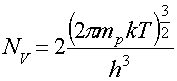
Логарифмируя выражение (13), получим

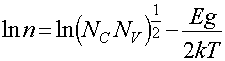                                      (14)

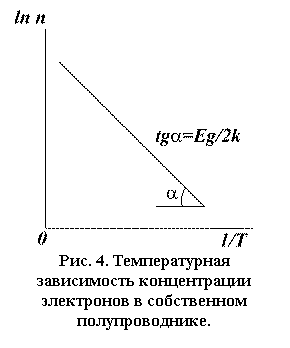Поскольку первое слагаемое в (14) практически от температуры не зависит, то зависимость ln n(1/Т) представляет собой прямую с угловым коэффициентом – Еg /(2k) (рис. 4).

Таким образом, концентрация носителей заряда в собственных полупроводниках зависит от ширины запрещенной зоны Eg и температуры Т. Для германия, например, Eg=0,72 эВ и концентрация носителей заряда при комнатной температуре составляет 10¹⁹ м^-3. Для кремния соответственно Eg = 1,21 эВ и n = p = 10¹⁶ м^-3.

Подвижность носителей заряда в полупроводниках определяется механизмами рассеяния носителей в кристалле. В идеальном полупроводнике с собственной проводимостью подвижность определяется рассеянием на тепловых колебаниях (фононах) решетки, поскольку идеальный собственный полупроводник – это, по определению, полупроводник без примесных атомов и рассеяние на примесных атомах отсутствует. Другой важный факт, определяющий температурную зависимость подвижности носителей в кристалле, связан с тем, является ли газ носителей невырожденным или вырожденным при данных условиях.

Если концентрация электронов в зоне проводимости или дырок в валентной зоне много меньше числа разрешенных состояний, то такой полупроводник называется невырожденным. Газ носителей (электронов или дырок) в таком полупроводнике также называют невырожденным. Для невырожденного газа вероятность того, что две частицы одновременно окажутся в одном квантовом состоянии мала, поэтому для таких частиц принцип Паули можно не учитывать и пользоваться для их статистического описания статистикой Максвелла-Больцмана. Полупроводник, в котором поведение свободных носителей описывается статистикой Ферми-Дирака, является вырожденным, а газ этих носителей также называют вырожденным. Условием невырожденности электронного газа является выполнение неравенства

                                               или                  ,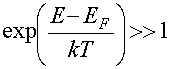

при котором статистика Ферми-Дирака переходит в статистику Максвелла-Больцмана. Это условие, в свою очередь, сводится к

                                              

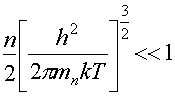
Таким образом, вырождение определяется концентрацией свободных носителей и температурой. Количественные оценки показывают, что для того, чтобы полупроводник при комнатной температуре был невырожденным, концентрация свободных носителей заряда в нем должна быть меньше 10²⁵ м⁻³. Собственные полупроводники удовлетворяют этому условию. В противоположность этому, электронный газ металлов в зоне проводимости всегда является вырожденным.

Температурная зависимость подвижности носителей заряда определяется температурной зависимостью длины свободного пробега носителей и их скоростью. Расчеты показывают, что для невырожденного газа носителей в области высоких температур подвижность обратно пропорциональна . Учитывая это, можно записать для подвижностей электронов и дырок

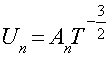
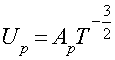                                                             (15)

гдеA_n и A_p  – некоторые независящие от температуры коэффициенты пропорциональности.

Подставляя (13) и (15) в (12) и логарифмируя полученное выражение, имеем

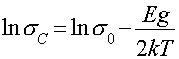                                                             (16)

 

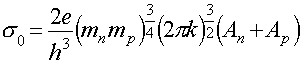
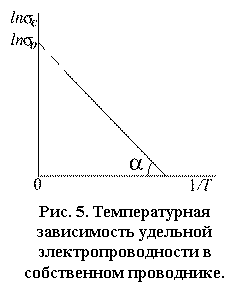График зависимости  от 1/Т представляет собой прямую линию (рис. 5), тангенс угла наклона которой к оси абсцисс пропорционален ширине запрещенной зоны. Это обстоятельство позволяет использовать данные по температурной зависимости электропроводности для нахождения ширины запрещенной зоны полупроводников.

Электропроводность примесного полупроводника называется примесной. Примеси могут весьма существенно влиять на электрические свойства полупроводников. Например, добавление в кремний бора в количестве одного атома на

10⁵ атомов кремния увеличивает проводимость при комнатной температуре в 1000 раз. Небольшая добавка примеси к полупроводнику называется легированием.

Удельная электропроводность примесных полупроводников, так же как и для собственных полупроводников, определяется концентрацией носителей заряда в зоне проводимости и их подвижностью. Для донорного полупроводника при низких температурах основным поставщиком электронов в зону проводимости являются донорные уровни примеси. За счет термического возбуждения электроны с донорных уровней переходят в зону проводимости. Концентрация электронов проводимости в донорном полупроводнике определяется выражением

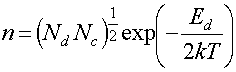,                                              (17)

где N_d – концентрация донорных уровней, E_d – разность энергии между дном зоны проводимости и донорным уровнем (энергия активации донорных уровней).

Повышение температуры приводит к истощению донорных уровней и при высоких температурах поведение донорного полупроводника аналогично поведению собственного полупроводника, когда приток электронов в зону проводимости происходит за счет их перехода из валентной зоны (см. уравнение 14).

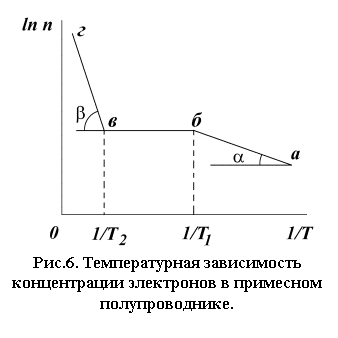Температурная зависимость концентрации электронов проводимости в донорном полупроводнике представлена схематически на рис. 6. Участок а-б соответствует температурной области примесной проводимости. Тангенс угла наклона  определяется энергией активации донорных уровней 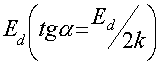. Температура истощения примеси

                                                           .

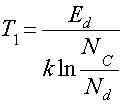В области б-в концентрация носителей заряда в зоне проводимости остается постоянной, т.к. примесные уровни истощены, а энергии теплового возбуждения еще недостаточно для перехода электронов из валентной зоны в зону проводимости. Электроны могут преодолеть запрещенную зону, начиная с температуры

.

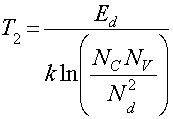При этом 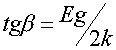 (рис. 6). Можно показать, что для дырок в акцепторном полупроводнике справедливы аналогичные результаты. Концентрация дырок в валентной зоне

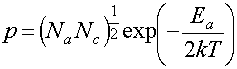                                   (18)

где E_a – концентрация акцепторных уровней; E_a – разность энергии между акцепторным уровнем и валентной зоной (энергия активации акцепторных уровней).

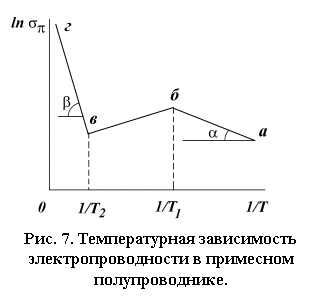Температурная зависимость удельной электропроводности примесного полупроводника схематически показана на рис. 7. Как показывают расчеты, не только для невырожденного газа носителей в собственном полупроводнике (см. уравнение 15), но и для примесной проводимости и для вырожденного газа носителей температурная зависимость подвижности значительно слабее, чем температурная зависимость концентрации носителей заряда в полупроводнике. Поэтому тангенсы углов наклона для области примесной проводимости (угол α) и собственной проводимости (угол β) определяется в основном, так же как и на рис. 6, энергиями активации примесных уровней и валентной зоны соответственно. Подвижность носителей существенное влияние оказывает на температурную зависимость электропроводности примесного полупроводника в области истощения примеси (участок б-в). В слаболегированных полупроводниках в области истощения примеси электропроводность даже уменьшается с ростом температуры, так как уменьшается подвижность носителей за счет механизма рассеяния их на фононах.

 

3. Методика измерений и экспериментальная установка

 

Бесконтактный метод измерения удельного электросопротивления связан с изменением добротности электрического колебательного контура за счет вихревых токов, наводимых в образце, помещенном в зазор катушки индуктивности контура.

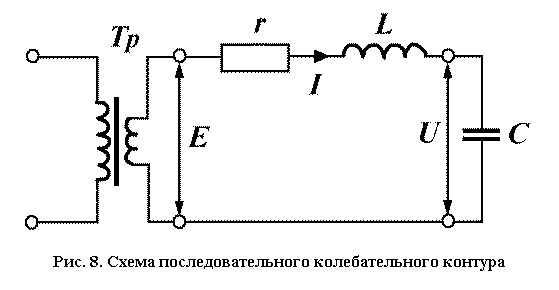
Добротность измерительной катушки индуктивности определяется с помощью стандартного измерителя добротности ВМ-560. Измеряемый индуктивный объект образует с конденсатором переменной емкости измерителя добротности последовательный колебательный контур (рис. 8). Электродвижущая сила вводится в контур через разделительный трансформатор Тр, сопротивление которого, вносимое в колебательный контур, пренебрежимо мало. Частота колебательного контура, как известно, определяется в основном значениями индуктивности L и емкости С, тогда как добротность контура Q, равная отношению энергии, запасенной в контуре, к энергии, теряемой контуром за один период, связана с величиной активного сопротивления R. Сопротивление R является общим сопротивлением потерь всего контура, однако, конструкция измерительного конденсатора выполнена так, что потери в нем всегда значительно меньше потерь в исследуемом объекте. Поэтому показания измерителя добротности можно считать практически свободными от влияния потерь в колебательном контуре измерительного блока в пределах погрешностей измерения.

Добротность контура, выраженная через сосредоточенные параметры

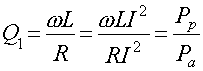                                                       (19)

здесь ω- частота электрических колебаний в контуре, I – сила тока в контуре, P_р – реактивная мощность, P_а – мощность активных потерь в контуре без образца. При внесении образца в контур знаменатель выражения (19) увеличивается на слагаемое P_ао, равное мощности активных потерь, вносимых образцом:

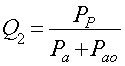,                                                              (20)

где Q₂ – добротность контура с образцом.

 

Выражение для мощности потерь, вносимых образцом, через величины Q₁ и Q₂ имеет вид

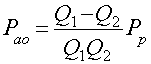.                                                       (21)

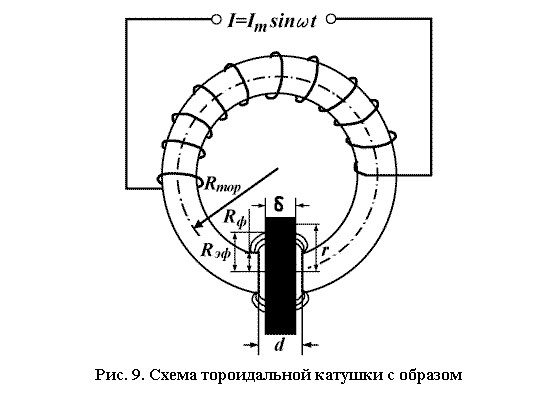
Активные потери в катушке с образцом увеличивается за счет индукционных токов, наводимых в проводящем образце переменным магнитным полем (рис. 9). Эти токи возникают вследствие явления электромагнитной индукции и образуют вихри, охватывающие изменяющееся магнитное поле. Такие токи называют вихревыми. Плотность вихревого тока определяется не только напряженностью электрического поля Е, но и удельным электрическим сопротивлением материала , , т.е. в конечном итоге потери в колебательном контуре определяются величиной . Величина напряженности электрического поля в данный момент на некотором круговом контуре l с радиусом r определяется из закона электромагнитной индукции

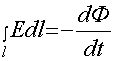                   или                                            (22)

здесь S - площадь поверхности, ограниченной контуром l. Тогда

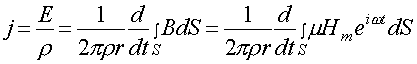                         (23)

здесь учтено, что , а , где - магнитная проницаемость среды, - частота переменного магнитного поля, H_m – его амплитуда.

Вытеснение поля из зазора образцом учитывается эффективным радиусом сечения тороида R_эф. С помощью несложных расчетов можно найти распределение плотности тока j, наведенного в образце полем тороидальной катушки [1]. Предполагается, что внешнее поле Н постоянно при r<R_эф и равно нулю при r>R_эф. Как показали эксперименты [1], эффективный радиус ферритового сердечника R_эф можно принять равным  (рис. 10).

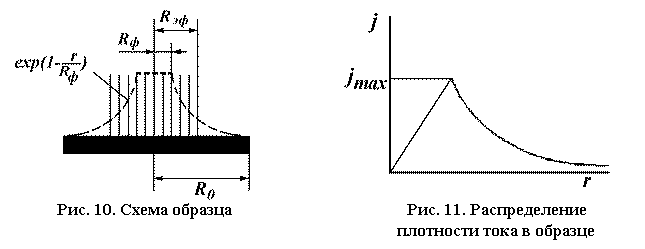
Для области r<R_эф

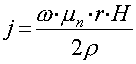,                                                           (24)

где  - магнитная проницаемость образца.

Для области r >R_эф

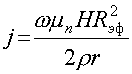.                                                            (25)

Для нахождения расчетной формулы определим величины P_р и P_ао. Реактивная мощность катушки индуктивности равна

,                                                                    (26)

где L – индуктивность катушки; I – ток катушки; ω – рабочая частота.

Индуктивность катушки с тороидальным сердечником

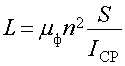                                                               (27)

здесь  – магнитная проницаемость ферромагнитного сердечника; n – число витков катушки; S – площадь сечения тора; Icp – средняя длина линии магнитной индукции в торе.

Из (26) и (27) получим

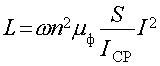.                                                     (28)

Мощность активных потерь можно определить, используя выражения (24) и (25)

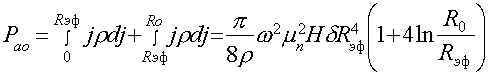                   (29)

здесь  – толщина образца.

Подставляя значения P_ао и P_р в формулу (21), получим расчетную формулу для определения удельного сопротивления образца.

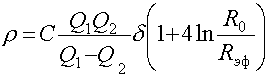,                                     (30)

где

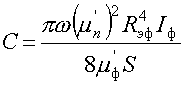
здесь  и  – динамические магнитные проницаемости образца и феррита соответственно.

Аппаратурная константа С определяется путем измерений Q₁ и Q₂ образца с известным удельным электросопротивлением (эталонный образец). Применение расчетной формулы (30), как показано в работе [1], справедливо при условии 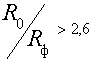. Точность метода, оцененная путем сравнительных измерений четырехзондовым методом, составляет приблизительно 20% при использовании стандартных приборов.

 

4. Порядок выполнения работы

 

1.      Внимательно ознакомиться с методикой эксперимента и описанием измерителя добротности ВМ-560.

2.      Получить разрешение преподавателя или инженера на включение прибора. Дать прогреться прибору в течении 15 мин.

3.      Подключить катушку индуктивности к клемме L_х на верхней панели измерителя добротности. В соответствии с описанием измерителя добротности ВМ-560 произвести калибровку прибора и настроить контур в резонанс.

4.      Произведите измерение добротности Q₁ катушки без образца.

5.      Вставьте в зазор тороидальной катушки эталонный образец с известным сопротивлением и измерьте Q₂ - добротность контура с образцом.

6.      Вычислите коэффициент С в соответствие с формулой (30).

7.      Вставьте в зазор катушки образцы с неизвестным удельным сопротивлением, измерьте для них Q₂, рассчитайте удельное сопротивление по формуле (30).

8.      Повторите, если необходимо, измерения для других образцов с неизвестными сопротивлениями.

9.      По полученным данным рассчитать удельную электропроводность, концентрацию носителей и время релаксации носителей заряда в исследованных материалах. Подвижность носителей принять равной 1300 см² / (В с).

10. Сделать выводы и составить отчет по проделанной работе.

 

5. Требования к отчету

 

Отчет должен содержать:

1.      Описание методики эксперимента и схему измерительной установки.

2.      Результаты измерений и расчетов.

3.      Анализ полученных результатов и выводы по работе.

 

6.Контрольные вопросы

 

1.      В чем ограниченность классической теории электропроводности металлов?

2.      Каковы особенности движения электронов в твердом теле?

3.      Объясните дрейф электронов в кристалле под действием внешнего постоянного электрического поля.

4.      Выведите формулу для удельной электропроводности металла.

5.      Дайте определение подвижности носителей заряда в кристалле. Чем определяется подвижность электронов в металле?

6.      Объясните температурную зависимость удельного электросопротивления металлов.

7.      Как зависит концентрация электронов от температуры в собственном полупроводнике?

8.      Какой полупроводник называется вырожденным?

9.      Как из графика температурной зависимости электропроводности собственного полупроводника определить ширину запрещенной зоны?

10. Объясните температурную зависимость концентрации электронов в примесном полупроводнике.

11. Чем отличается температурные зависимости электропроводности собственного и примесного полупроводников?

12. Объясните схему экспериментальной установки для бесконтактного метода измерения удельного электросопротивления полупроводниковых пластин.

13. Почему добротность контура зависит от удельного электросопротивления образца?

14. Каким образом в эксперименте определяется постоянная установки С ?

 

7. Литература

 

1.      Сурин Ю.В., Шимко В.И., Матвеев В.В. Бесконтактный метод измерения удельного сопротивления пластин полупроводников и эпитаксиальных слоев.- Заводская лаборатория, 1966, т.32, N9, С.1086-1088.

2.      Епифанов Г.И., Момма Ю.А. Твердотельная электроника-М.: Высш. школа., 1986.-304С.

3.      Киттель Ч. Введение в физику твердого тела. -М.: Наука, 1978, 792С.

4.      Фридрихов С.А., Мовнин С.М. Физические основы электронной техники.-М.: Высш. школа, 1982, 608 с.

5.      Соболев В.Д. Физические основы электронной техники. –М.: Высш. школа, 1979, 448 с.