Эмиссионная электроника изучает явления, связанные с испусканием (эмиссией) электронов конденсированной средой. Электронная эмиссия возникает в случаях, когда часть электронов тела приобретает в результате внешнего воздействия энергию, достаточную для преодоления потенциального барьера на его границе, или если внешнее электрическое поле делает его "прозрачным" для части электронов. В зависимости от природы внешнего воздействия различают:

термоэлектронную эмиссию (нагревание тел);
вторичную электронную эмиссию (бомбардировка поверхности электронами);
ионно-электронную эмиссию (бомбардировка поверхности ионами);
фотоэлектронную эмиссию (электромагнитное облучение);
экзоэлектронную эмиссию (механическая, термическая и другие виды обработки поверхности);
автоэлектронную эмиссию (внешнее электрическое поле) и др.

Во всех явлениях, где необходимо учитывать либо выход электрона из кристалла в окружающее пространство, либо переход из одного кристалла в другой, определяющее значение приобретает характеристика, носящая название "Работа выхода". Работа выхода определяется как минимальная энергия, требуемая, чтобы извлечь электрон из твердого тела и поместить его в точку, где его потенциальная энергия условно принимается равной нулю. Кроме описания различных эмиссионных явлений, понятие работы выхода играет важную роль при объяснении возникновения контактной разности потенциалов при контакте двух металлов, металла с полупроводником, двух полупроводников, а также гальванических явлений.

Методические указания состоят из двух частей. Первая часть содержит основные теоретические сведения по эмиссионным явлениям в твердых телах. Основное внимание уделено явлению термоэлектронной эмиссии. Во второй части приведено описание лабораторных работ, посвященных экспериментальному изучению термоэлектронной эмиссии, исследованию контактной разности потенциалов и распределении работы выхода по поверхности образца.

Часть 1. Основные теоретические сведения

1. Работа выхода электрона. Влияние на работу выхода состояния поверхности

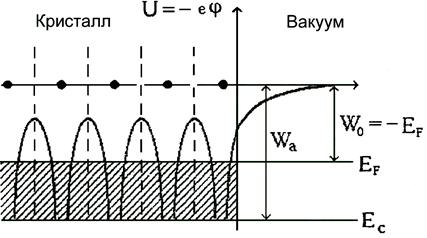
То обстоятельство, что электроны удерживаются внутри твердого тела, указывает на то, что в поверхностном слое тела возникает задерживающее поле, препятствующее электронам выходить из него в окружающий вакуум. Схематическое изображение потенциального барьера на границе твердого тела дано на рис. 1. Чтобы покинуть кристалл, электрон должен совершить работу, равную работе выхода. Различают термодинамическую и внешнюю работы выхода.

Термодинамической работой выхода называют разницу между энергией нулевого уровня вакуума и энергией Ферми твердого тела.

Внешняя работа выхода (или электронное сродство) – это разность между энергией нулевого уровня вакуума и энергией дна зоны проводимости (рис. 1).

Рис. 1. Форма кристаллического потенциала U вдоль линии расположения ионов в кристалле и в приповерхностной области кристалла: положения ионов отмечены точками на горизонтальной линии; φ=-U/е – потенциал работы выхода; Е_F – энергия Ферми (отрицательная); Е_C – энергия дна зоны проводимости; W_O – термодинамическая работа выхода; W_a – внешняя работа выхода; заштрихованная область условно изображает заполненные электронные состояния

Можно указать две основные причины возникновения потенциального барьера на границе твердого тела и вакуума. Одна из них связана с тем, что электрон, вылетевший из кристалла, индуцирует на его поверхности положительный электрический заряд. Возникает сила притяжения между электроном и поверхностью кристалла (сила электрического изображения, см. разд. 5, рис. 12), стремящаяся вернуть электрон обратно в кристалл. Другая причина связана с тем, что электроны за счет теплового движения могут пересекать поверхность металла и удаляться от него на небольшие расстояния (порядка атомных). Они образуют над поверхностью отрицательно заряженный слой. На поверхности кристалла в этом случае после выхода электронов формируется положительно заряженный слой ионов. В результате образуется двойной электрический слой. Он не создает поля во внешнем пространстве, зато на преодоление электрического поля внутри самого двойного слоя также требуется произвести работу.

Значение работы выхода для большинства металлов и полупроводников составляет несколько электрон-вольт. Например, для лития работа выхода равна 2,38 эВ, железа – 4,31 эВ, германия – 4,76 эВ, кремния – 4,8 эВ. В значительной степени величина работы выхода определяется кристаллографической ориентацией грани монокристалла, с которой происходит эмиссия электронов. Для (110)-плоскости вольфрама работа выхода составляет 5,3 эВ, для (111) и (100)-плоскостей эти значения равны соответственно 4,4 эВ и 4,6 эВ.

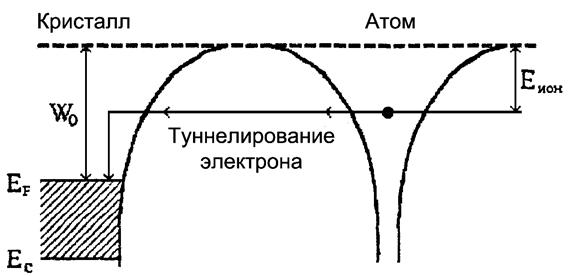
Рис. 2. Энергетическая диаграмма для электронов металла и для валентного электрона в атоме

Большое влияние на работу выхода оказывают тонкие слои, нанесенные на поверхность кристалла. Атомы или молекулы, осевшие на поверхность кристалла, часто отдают электрон в него или принимают электрон от него и становятся ионами. На рис. 2 показана энергетическая диаграмма металла и изолированного атома для случая, когда термодинамическая работа выхода электрона из металла W₀ больше, чем энергия ионизации Е_ион осаждающегося на его поверхность атома, В этой ситуации электрону атома энергетически выгодно протуннелировать в металл и опуститься в нем к уровню Ферми. 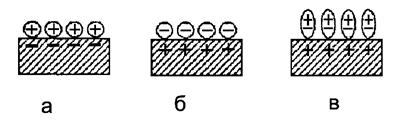Поверхность металла, покрытая такими атомами, заряжается отрицательно и образует с положительными ионами двойной электрический слой, поле которого будет уменьшать работу выхода из металла. На рис. З, а показан кристалл вольфрама, покрытый монослоем цезия. Здесь реализуется ситуация, рассмотренная выше, так как энергия Е_ион цезия (3,9 эВ) меньше работы выхода вольфрама (4,5 эВ). В экспериментах работа выхода уменьшается более чем в три раза. Противоположная ситуация наблюдается, если вольфрам покрыт атомами кислорода (рис. 3 б). Поскольку связь валентных электронов в кислороде сильнее, чем в вольфраме, то при адсорбции кислорода на поверхности вольфрама образуется двойной электрический слой, увеличивающий работу выхода из металла. Наиболее часто реализуется случай, когда осевший на поверхность атом не отдает полностью свой электрон металлу или принимает в себя лишний электрон, а деформирует свою электронную оболочку так, что адсорбированные на поверхности атомы поляризуются и становятся электрическими диполями (рис. 3 в). В зависимости от ориентации диполей работа выхода металла уменьшается (ориентация диполей соответствует рис. 3 в) или увеличивается.

2. Явление термоэлектронной эмиссии

Термоэлектронная эмиссия является одним из видов эмиссии электронов поверхностью твердого тела. В случае термоэлектронной эмиссии внешнее воздействие связано с нагреванием твердого тела.

Явлением термоэлектронной эмиссии называется испускание электронов нагретыми телами (эмиттерами) в вакуум или другую среду.

Рис. 3 Схематическое изображение поверхности металла, покрытой положительными (а), отрицательными (б) ионами или поляризованными частицами (в)

В условиях термодинамического равновесия число электронов n(Е), имеющих энергию в интервале от Е до Е+dЕ, определяется статистикой Ферми-Дирака:

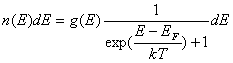, (1)

где g(Е) – число квантовых состояний, соответствующих энергии Е; Е_F – энергия Ферми; k – постоянная Больцмана; Т – абсолютная температура.

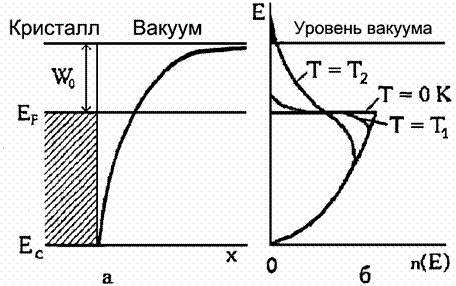
Рис. 4. Энергетическая схема кристалла (а) и кривые распределения электронов по энергии при разных температурах (б). Заштрихованная область выше уровня вакуума – "хвост" кривой распределения при Т=Т₂

На рис. 4 показаны энергетическая схема металла и кривые распределения электронов по энергиям при Т=0 К, при низкой температуре Т₁ и при высокой температуре Т₂. При 0 К энергия всех электронов меньше энергии Ферми. Ни один из электронов покинуть кристалл не может и никакой термоэлектронной эмиссии не наблюдается. С увеличением температуры возрастает число термически возбужденных электронов, способных выйти из металла, что обусловливает явление термоэлектронной эмиссии. На рис. 4 это иллюстрируется тем, что при Т=Т₂ "хвост" кривой распределения заходит за нулевой уровень потенциальной ямы. Это свидетельствует о появлении электронов, обладающих энергией, превышающей высоту потенциального барьера.

Для металлов работа выхода составляет несколько электрон-вольт. Энергия kТ даже при температуре в тысячи Кельвинов составляет доли электрон-вольт. Для чистых металлов значительная эмиссия электронов может быть получена при температуре порядка 2000 К. Например, в чистом вольфраме заметную эмиссию можно получить при температуре 2500 К.

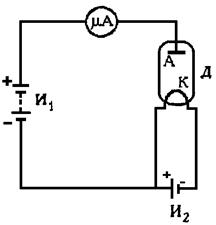
Рис. 5. Схема включения диода для изучения термоэлектронного тока: Д - вакуумный диод; К - катод: А - анод;И₁ - источник анодного напряжения; И₂ - источник накала катода; μА - микроамперметр

Для исследования термоэлектронной эмиссии необходимо создать у поверхности нагретого тела (катода) электрическое поле, ускоряющее электроны для их удаления (отсасывания) от поверхности эмиттера. Под действием электрического поля эмиттированные электроны приходят в движение и образуется электрический ток, который называется термоэлектронным. Для наблюдения термоэлектронного тока обычно используют вакуумный диод – электронную лампу с двумя электродами. Катодом лампы служит нить из тугоплавкого металла (вольфрама, молибдена и др.), накаливаемая электрическим током. Анод обычно имеет форму металлического цилиндра, окружающего накаливаемый катод. Для наблюдения термоэлектронного тока диод включают в цепь, изображенную на рис. 5. 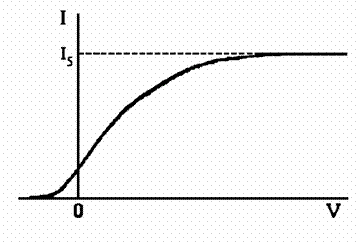Очевидно, что сила термоэлектронного тока должна расти с увеличением разности потенциалов V между анодом и катодом. Однако это возрастание идет не пропорционально V (рис. 6). По достижении определенного напряжения нарастание термоэлектронного тока практически прекращается. Предельное значение термоэлектронного тока при данной температуре катода называется током насыщения. Величина тока насыщения определяется количеством термоэлектронов, которые в состоянии выйти с поверхности катода за единицу времени. В этом случае все электроны, поставляемые в результате термоэлектронной эмиссии из катода, задействованы для образования электрического тока.

Рис.6. Вольт-амперная характеристика вакуумного диода

3. Зависимость термоэлектронного тока от температуры. Формула Ричардсона-Дешмана

Рис. 7. К расчету плотности термоэлектронного тока

При вычислении плотности термоэлектронного тока будем пользоваться моделью электронного газа и применим к нему статистику Ферми-Дирака. Очевидно, что плотность термоэлектронного тока определяется плотностью облака электронов вблизи поверхности кристалла, которая описывается формулой (1). Перейдем в этой формуле от распределения электронов по энергиям к распределению электронов по импульсам. При этом учтем, что разрешенные значения волнового вектора электрона k в k-пространстве распределены равномерно так, что на каждое значение k приходится объем 8p³ (для объема кристалла, равного единице). Учитывая, что импульс электрона p=ћk получим, что число квантовых состояний в элементе объема пространства импульсов dp_x•dp_y•dp_z будет равно

(2)

Двойка в числителе формулы (2) учитывает два возможных значения спина электрона.

Направим ось z прямоугольной системы координат нормально к поверхности катода (рис. 7). Выделим на поверхности кристалла площадку единичной площади и построим на ней, как на основании, прямоугольный параллелепипед с боковым ребром v_z=p_z/m_n (m_n – эффективная масса электрона). Электроны дают клад в плотность тока насыщения компонентой v_z скорости по оси z. Вклад в плотность тока от одного электрона равен

(3)

где е – заряд электрона.

Число электронов в параллелепипеде, скорости которых заключены в рассматриваемом интервале:

(4)

Чтобы при эмиссии электронов кристаллическая решетка не разрушалась, из кристалла должна выходить ничтожная часть электронов. Для этого, как показывает формула (4), должно выполняться условие Е-Е_F >> kТ. Для таких электронов в знаменателе формулы (4) единицей можно пренебречь. Тогда эта формула преобразуется к виду

(5)

Найдем теперь число электронов dN в рассматриваемом объеме, z-составляющая импульса которых заключена между р_z и р_z+dp_z. Для этого предыдущее выражение надо проинтегрировать по р_x и р_y в пределах от –∞ до +∞. При интегрировании следует учесть, что

и воспользоваться табличным интегралом

, .

В результате получим

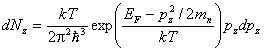. (6)

Теперь, учитывая (3), найдем плотность термоэлектронного тока, создаваемого всеми электронами параллелепипеда. Для этого выражение (6) надо проинтегрировать для всех электронов, кинетическая энергия которых на уровне Ферми E≥E_F+W₀.Только такие электроны могут выходить из кристалла и только они играют роль в вычислении термотока. Составляющая импульса таких электронов вдоль оси Z должна удовлетворять условию

Следовательно, плотность тока насыщения

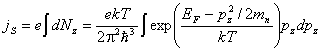. (7)

Интегрирование производится для всех значений . Введем новую переменную интегрирования

Тогда p_zdp_z=m_ndu и

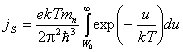. (8)

В результате получим

, (9)

или

, (10)

где постоянная

Равенство (10) называется формулой Ричардсона-Дешмана. Измеряя плотность термоэлектронного тока насыщения, можно по этой формуле вычислить постоянную А и работу выхода W₀. Для экспериментальных расчетов формулу Ричардсона-Дешмана удобно представить в виде

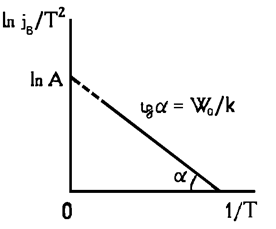
В этом случае на графике зависимость ln(j_s/T²) от 1/Т выражается прямой линией. По пересечению прямой с осью ординат вычисляют ln А, а по углу наклона прямой определяют работу выхода (рис. 8).

Рис. 8. Зависимость плотности термоэмиссионного тока от температуры

4. Контактная разность потенциалов

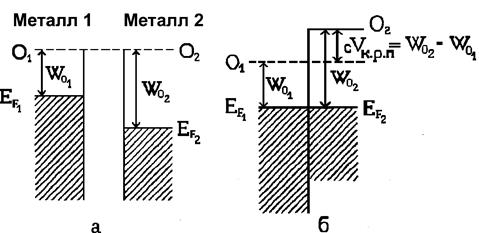
Рассмотрим процессы, происходящие при сближении и контакте двух электронных проводников, например двух металлов, с разными работами выхода. Энергетические схемы этих металлов показаны на рис. 9. Пусть Е_F1 и Е_F2 – энергия Ферми для первого и второго металла соответственно, а W₀₁ и W₀₂ – их работы выхода. В изолированном состоянии у металлов одинаков уровень вакуума и, следовательно, разные уровни Ферми. Предположим для определенности, что W₀₁<W₀₂, тогда уровень Ферми первого металла будет выше, чем второго (рис. 9 а). При контакте этих металлов против занятых электронных состояний в металле 1 находятся свободные энергетические уровни металла 2. Поэтому при контакте этих проводников возникает результирующий поток электронов из проводника 1 в проводник 2. Это приводит к тому, что первый проводник, теряя электроны, заряжается положительно, а второй проводник, приобретая дополнительный отрицательный заряд, заряжается отрицательно. Вследствие зарядки все энергетические уровни металла 1 смещаются вниз, а металла 2 – вверх. Процесс смещения уровней и процесс перехода электронов из проводника 1 в проводник 2 будет продолжаться до тех пор, пока уровни Ферми обоих проводников не выровняются (рис. 9 б). Как видно из этого рисунка, равновесному состоянию соответствует разность потенциалов между нулевыми уровнями проводников 0₁ и 0₂:

. (11)

Рис. 9. Возникновение контактной разности потенциалов между двумя металлами

Разность потенциалов V_К.Р.П называется контактной разностью потенциалов. Следовательно, контактная разность потенциалов определяется разностью работ выхода электронов из контактирующих проводников. Полученный результат справедлив для любых способов обмена двух материалов электронами, в том числе и путем термоэлектронной эмиссии в вакууме, через внешнюю цепь и т.д. Аналогичные результаты получаются при контакте металла с полупроводником. Между металлами и полупроводником возникает контактная разность потенциалов, имеющая примерно тот же порядок величины, что и в случае контакта двух металлов (приблизительно 1 В). Различие состоит лишь в том, что если в проводниках вся контактная разность потенциалов приходится практически на зазор между металлами, то при контакте металла с полупроводником вся контактная разность потенциалов приходится на полупроводник, в котором образуется достаточно большой слой, обогащенный или обедненный электронами. Если этот слой обеднен электронами (в случае, когда работа выхода полупроводника n-типа меньше работы выхода металла), то такой слой называют блокирующим и такой переход будет обладать выпрямляющими свойствами. Потенциальный барьер, возникающий в выпрямляющем контакте металла с полупроводником, называют барьером Шоттки, а диоды, работающие на его основе, – диодами Шоттки.

5. Вольт-амперная характеристика термокатода при малых плотностях тока эмиссии. Эффект Шоттки

Если между термокатодом и анодом диода (рис. 5) создать разность потенциалов V, препятствующую движению электронов к аноду, то на анод смогут попасть лишь те из них, которые вылетели из катода с запасом кинетической энергии не меньше энергии электростатического поля между анодом и катодом, т.е. –еV (V<0). Для этого их энергия в термокатоде должна быть не меньше W₀–еV. Тогда, заменив в формуле Ричардсона-Дешмана (10) W₀ на W₀–еV, получим следующее выражение для плотности тока термоэмиссии:

, (12)

здесь j_S – плотность тока насыщения. Логарифмируем это выражение

. (13)

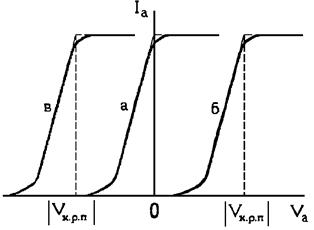
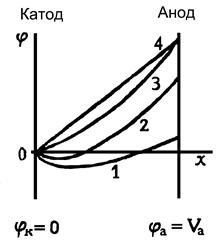
При положительном потенциале на аноде все электроны, покидающие термокатод, попадают на анод. Поэтому ток в цепи меняться не должен, оставаясь равным току насыщения. Таким образом, вольт-амперная характеристика (ВАХ) термокатода будет иметь вид, представленный на рис. 10 (кривая а).

Рис. 10. Сдвиг вольт-амперной характеристики диода в зависимости от контактной разности потенциалов между катодом и анодом: а – W_a= W_k; б – W_a > W_k; в – W_a < W_k

Подобная ВАХ наблюдается лишь при относительно малых плотностях тока эмиссии и высоких положительных потенциалах на аноде, когда вблизи эмиттирующей поверхности не возникает значительного объемного заряда электронов. Вольт-амперная характеристика термокатода с учетом пространственного заряда рассмотренная в разд. 6.

Отметим еще одну важную особенность ВАХ при малых плотностях тока эмиссии. Вывод о том, что термоток достигает насыщения при V=0, справедлив только для случая, когда материалы катода и анода обладают одинаковой термодинамической работой выхода. Если работы выхода катода и анода не равны между собой, то между анодом и катодом появляется контактная разность потенциалов. В этом случае даже при отсутствии внешнего электрического поля (V=0) между анодом и катодом существует электрическое поле, обусловленное контактной разностью потенциалов. Например, если W_0к<W_0а то анод будет заряжен отрицательно относительно катода. Для уничтожения контактной разности потенциалов на анод следует подать положительное смещение. Поэтому вольт-амперная характеристика термокатода сдвигается на величину контактной разности потенциалов в сторону положительного потенциала (рис. 10, кривая б). При обратном соотношении между W_0к и W_0а направление сдвига ВАХ противоположно (кривая в на рис. 10).

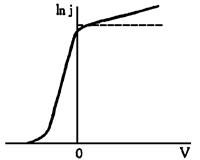
Вывод о независимости плотности тока насыщения при V>0 сильно идеализирован. В реальных ВАХ термоэлектронной эмиссии наблюдается небольшое увеличение тока термоэлектронной эмиссии с ростом V в режиме насыщения, что связано с эффектом Шоттки (рис. 11).

Эффект Шоттки – это уменьшение работы выхода электронов из твердых тел под действием внешнего ускорявшего электрического поля.

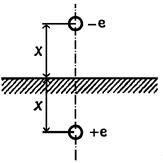
Для объяснения эффекта Шоттки рассмотрим силы, действующие на электрон вблизи поверхности кристалла. В соответствии с законом электростатической индукции на поверхности кристалла индуцируются поверхностные заряды противоположного знака, определяющие взаимодействие электрона с поверхностно кристалла. В соответствии с методом электрических изображений действие реальных поверхностных зарядов на электрон заменяется действием фиктивного точечного положительного заряда +е, расположенного на таком же расстоянии от поверхности кристалла, что и электрон, но с противоположной стороны поверхности (рис. 12). Тогда, в соответствии с законом Кулона, сила взаимодействия двух точечных зарядов

Рис. 11 Вольт-амперная характеристика при малых плотностях тока термоэмиссии с учетом эффекта Шоттки

Рис. 12. К вычислению силы электрического изображения

, (14)

здесь ε_o – электрическая постоянная: х – расстояние между электроном и поверхностью кристалла.

Потенциальная энергия электрона в поле силы электрического изображения, если отсчет вести от нулевого уровня вакуума, равна

. (15)

Потенциальная энергия электрона во внешнем ускоряющем электрическом поле Е

. (16)

Полная потенциальная энергия электрона

. (17)

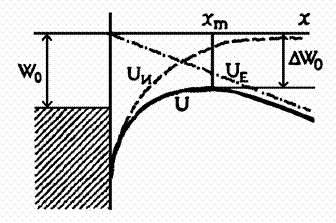
Рис. 13. Влияние внешнего поля на высоту и форму потенциального барьера

Графическое нахождение полной энергии электрона, находящегося вблизи поверхности кристалла, приведено на рис. 13, на котором наглядно видно уменьшение работы выхода электрона из кристалла. Суммарная кривая потенциальной энергии электрона (сплошная кривая на рис. 13) достигает максимума в точке x_m:

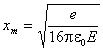. (18)

Эта точка отстоит от поверхности на расстоянии 10 Å при напряженности внешнего поля »3×10⁶ В/см.

В точке х_m суммарная потенциальная энергия, равная понижению потенциального барьера (и, следовательно, уменьшению работы выхода),

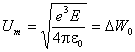. (19)

В результате эффекта Шоттки ток термодиода при положительном напряжении на аноде растет с ростом анодного напряжения. Этот эффект проявляется не только при эмиссии электронов в вакуум, но и при движении их через контакты металл-полупроводник или металл- диэлектрик.

6. Токи в вакууме ограниченные пространственным зарядом. Закон «трех вторых»

При больших плотностях тока термоэлектронной эмиссии на вольт-амперную характеристику существенное влияние оказывает объемный отрицательный заряд, возникающий между катодом и анодом. Этот объемный отрицательный заряд препятствует достижению вылетевшим из катода электронам анода. Таким образом, ток анода оказывается меньше, чем ток эмиссии электронов с катода. При приложении к аноду положительного потенциала дополнительный потенциальный барьер у катода, создаваемый объемным зарядом, понижается и анодный ток растет. Такова качественная картина влияния пространственного заряда на вольт-амперную характеристику термодиода. Теоретически этот вопрос был исследован Ленгмюром в 1913 г.

Вычислим при ряде упрощающих предположений зависимость тока термодиода от приложенной между анодом и катодом внешней разности потенциалов и найдем распределение поля, потенциала и концентрации электронов между анодом и катодом при учете пространственного заряда.

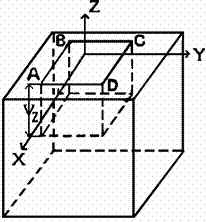
Рис. 14. К выводу закона "трех вторых"

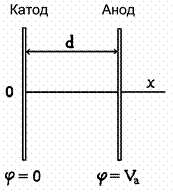
Допустим, что электроды диода плоские. При небольшом расстоянии между анодом и катодом d их можно считать бесконечно большими. Начало координат поместим на поверхности катода, а ось X направим перпендикулярно этой поверхности в сторону анода (рис. 14). Температуру катода будем поддерживать постоянной и равной Т. Потенциал электростатического поля j, существующего в пространстве между анодом и катодом, будет функцией только одной координаты х. Он должен удовлетворять уравнению Пуассона

, (20)

здесь r – объемная плотность заряда; n – концентрация электронов; j, r и n являются функциями координаты х.

Учитывая, что плотность тока между катодом и анодом

а скорость электрона v можно определить из уравнения

где m – масса электрона, уравнение (20) можно преобразовать к виду

, . (21)

Это уравнение надо дополнить граничными условиями

, . (22)

Эти граничные условия следуют из того, что потенциал и напряженность электрического поля у поверхности катода должны обращаться в нуль. Умножая обе части уравнения (21) на dj/dx, получим

. (23)

Учитывая, что

(24а)

и 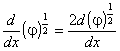, (24b)

запишем (23) в виде

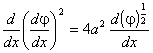. (25)

Теперь можно проинтегрировать обе части уравнения (25) по х в пределах от 0 до того значения x, при котором потенциал равен j. Тогда, учитывая граничные условия (22) получим

(26)

или

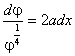. (27)

Интегрируя обе части (27) в пределах от х=0, j=0 до х=1, j=V_a, получим

. (28)

Возведя обе части равенства (28) в квадрат и выражая плотность тока j из а согласно (21), получим

, (29)

где

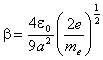. (30)

Формула (29) называется "законом трех вторых" Ленгмюра.

Этот закон справедлив для электродов произвольной формы. От формы электродов зависит выражение для численного коэффициента. Полученные выше формулы позволяют вычислить распределения потенциала, напряженности электрического поля и плотности электронов в пространстве между катодом и анодом. Интегрирование выражения (26) в пределах от х=0 до того значения, когда потенциал равен j, приводит к соотношению

, (31)

т.е. потенциал меняется пропорционально расстоянию от катода х в степени 4/3. Производная dj/dx характеризует напряженность электрического поля между электродами. Согласно (26), величина напряженности электрического поля Е ~х¹^/9. Наконец, концентрация электронов

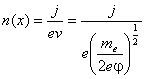(32)

и, согласно (31) n(x)~ (1/x)^2/9.

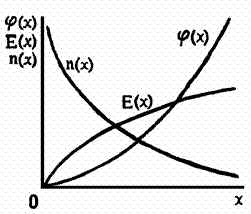
Рис 15. Влияние объемного заряда на распределение потенциала между анодом и катодом при разных значениях анодного напряжения

Зависимости j(х), Е(х) и n(х) приведены на рис. 15. Если х→0, то концентрация устремляется к бесконечности. Это является следствием пренебрежения тепловыми скоростями электронов у катода. В реальной ситуации при термоэлектронной эмиссии электроны покидают катод не с нулевой скоростью, а с некоторой конечной скоростью эмиссии. В этом случае анодный ток будет существовать даже в том случае, если вблизи катода имеется небольшое обратное электрическое поле. Следовательно, объемная плотность заряда может измениться до таких значений, при которых потенциал вблизи катода уменьшится до отрицательных значений (рис 16). При увеличении анодного напряжения минимум потенциала уменьшается и приближается к катоду (кривые 1 и 2 на рис. 16). При достаточно большом напряжении на аноде минимум потенциала сливается с катодом, напряженность поля у катода становится равной нулю и зависимость j(х) приближается к (29), рассчитанной без учета начальных скоростей электронов (кривая 3 на рис. 16). При больших анодных напряжениях пространственный заряд почти полностью рассасывается и потенциал между катодом и анодом меняется по линейному закону (кривая 4, рис. 16).

Рис 16. Влияние объемного заряда на распределение потенциала между анодом и катодом

Рис.17. Распределение потенциала при расчете плотности тока по формуле (33)

Таким образом, распределение потенциала в межэлектродном пространстве при учете начальных скоростей электронов значительно отличается от того, который положен в основу идеализированной модели при выводе закона "трех вторых". Это приводит к изменению и зависимости плотности анодного тока. Расчет, учитывающий начальные скорости электронов, для случая распределения потенциала, показанного на рис. 17, и для цилиндрически электродов дает следующую зависимость для полного тока термоэлектронной эмиссии I (I=jS, где S – площадь поперечного сечения термотока):

. (33)

Параметры x_m и V_m определяются видом зависимости j(х), смысл их понятен из рис. 17. Параметр х_m равен расстоянию от катода, на котором потенциал достигает своего минимального значения = V_m. Множитель C(x_m), кроме x_m, зависит от радиусов катода и анода. Уравнение (33) справедливо при небольших изменениях анодного напряжения, т.к. и х_m и V_m, как это обсуждалось выше, зависят от анодного напряжения.

Таким образом, закон "трех вторых" не имеет универсального характера, он справедлив лишь в сравнительно узком интервале напряжений и токов. Однако он является наглядным примером нелинейного соотношения между силой тока и напряжением электронного прибора. Нелинейность вольт-амперной характеристики является наиболее важной особенностью многих элементов радио- и электротехнических схем, включая элементы твердотельной электроники.

Часть 2. Лабораторные работы

7. Экспериментальная установка для изучения термоэлектронной эмиссии

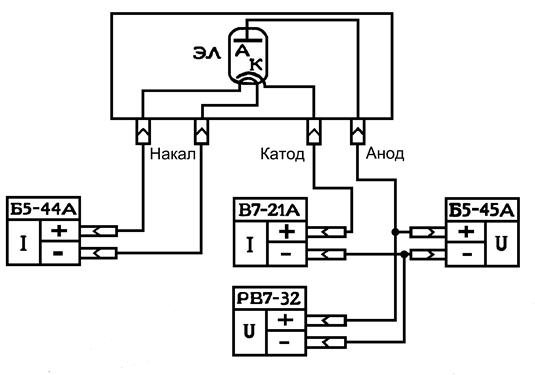
Рис.18. Блок-схема экспериментальной установки

Лабораторные работы №1 и 2 выполняется на одной лабораторной установке, реализованной на базе универсального лабораторного стенда. Схема установки представлена на рис. 18. В измерительной секции располагается вакуумный диод ЭЛ с катодом прямого или косвенного накала. На переднюю панель измерительной секции выведены контакты нити накала "Накал", анода "Анод" и катода "Катод". Источником накала служит стабилизированный источник постоянного тока типа В5-44А. Значок I на схеме обозначает, что источник работает в режиме стабилизации тока. С порядком работы с источником постоянного тока можно ознакомиться по техническому описанию и инструкции по эксплуатации для этого прибора. Аналогичные описания имеются для всех электроизмерительных приборов, используемых в лабораторных работах. В анодную цепь включены стабилизированный источник постоянного тока Б5-45А и универсальный цифровой вольтметр В7-21А, используемый в режиме измерения постоянного тока для измерения анодного тока термодиода. Для измерения анодного напряжения и тока накала катода можно использовать встроенные в источник питания, приборы или подключить для более точного измерения напряжения на катоде дополнительный вольтметр РВ7-32.

В измерительной секции могут находиться вакуумные диоды с разными рабочими тогами накала катода. При номинальном токе накала диод работает в режиме ограничения анодного тока пространственным зарядом. Этот режим необходим для выполнения лабораторной работы №1. Лабораторная работа №2 выполняется при пониженных токах накала, когда влияние пространственного заряда несущественно. При установке тока накала следует быть особенно внимательным, т.к. превышение тока накала над его номинальным значением для данной электронной лампы приводит к перегоранию нити накала катода и выводу диода из строя. Поэтому при подготовке к работе обязательно уточните у преподавателя или инженера величину рабочего тока накала используемого в работе диода, данные обязательно запишите в рабочую тетрадь и используйте при составлении отчета по лабораторной работе.

8. Лабораторная работа №1. Изучение влияния пространственного заряда на вольт-амперную характеристику термотока

Цель работы: экспериментальное изучение зависимости тока термоэлектронной эмиссии от анодного напряжения, определение показателя степени в законе "трех вторых".

Вольт-амперная характеристика тока термоэлектронной эмиссии описывается законом "трех вторых" (см. разд. 6). Такой режим работы диода возникает при достаточно больших токах накала катода. Обычно при номинальном токе накала ток вакуумного диода ограничен пространственным зарядом.

Экспериментальная установка для выполнения данной лабораторной работы описана в разд. 7. В работе необходимо снять вольт-амперную характеристику диода при номинальном токе накала. Значение рабочего тока шкала используемой электронной лампы следует взять у преподавателя или инженера и записать в рабочую тетрадь.

Порядок выполнения работы

Для выполнения лабораторной работы необходимо:

1. Ознакомиться с описанием и порядком работы с приборами, необходимыми для работы экспериментальной установки. Собрать схему согласно рис 18. Установку можно включать в сеть только после проверки правильности собранной схемы инженером или преподавателем.

2. Включить источник питания тока накала катода и установить требуемый ток накала. Поскольку при изменении тока накала изменяется температура и сопротивление нити накала, что, в свою очередь, ведет к изменению тока накала, регулировку необходимо вести методом последовательных приближений. После окончания регулировки необходимо выждать приблизительно 5 мин, чтобы ток накала и температура катода стабилизировались.

3. Включить в цепь анода источник постоянного напряжения и, изменяя напряжение на аноде, снять по точкам вольт-амперную характеристику. Вольт-амперную характеристику снимать в диапазоне 0...25 В, через каждые 0,5…1 В.

4. Результаты измерений представить на графике в координатах ln I_a(V_a), где I_a – анодный ток, V_a – анодное напряжение.

5. Если диапазон изменения анодного напряжения взять небольшим, то величины x_m, C(x,n) и V_m, входящие в формулу (33), можно принять постоянными. При больших V_a величиной V_m можно пренебречь. В результате формула (33) преобразуется к виду (после перехода от плотности термотока j к его полному значению I)

. (34)

6. Из формулы (34) определить значение С для трех максимальных значений анодного напряжения на вольт-амперной характеристике. Вычислить среднее арифметическое полученных значений. Подставив это значение в формулу (33), определить значение V_m для трех минимальных значений напряжения на аноде и вычислить среднее арифметическое значение V_m.

7. Пользуясь полученным значением V_m, построить график зависимости ln I_a от ln(V_a+|V_m|). Определить по тангенсу угла этого графика показатель степени зависимости I_a(V_a+V_m). Он должен быть близок к 1,5.

8. Оформить отчет по работе.

Требования к отчету

Отчет оформляется на стандартном листе бумаги формата А4 и должен содержать:

1. Основные сведения по теории.

2. Схему экспериментальной установки и ее краткое описание.

3. Результаты измерений и расчетов.

4. Анализ полученных экспериментальных результатов.

5. Выводы по работе.

Контрольные вопросы

1. Что называется явлением термоэлектронной эмиссии? Дайте определение работы выхода электрона. В чем различие термодинамической и внешней работы выхода?

2. Объясните причины возникновения потенциального барьера на границе твердое тело – вакуум.

3. Объясните, исходя из энергетической схемы металла и кривой распределения электронов по энергиям, термоэмиссию электронов из металла.

4. При каких условиях наблюдается термоэлектронный ток? Как можно наблюдать термоэлектронный ток? Как зависит ток термодиода от приложенного электрического поля?

5. Сформулируйте закон Ричардсона-Дешмана. Объясните физический смысл входящих в этот закон величин.

6. Объясните качественную картину влияния объемного отрицательного заряда на вольт-амперную характеристику термодиода. Сформулируйте закон "трех вторых" Ленгмюра.

7. Каковы распределения потенциала, напряженности электрического поля и плотности электронов в пространстве между катодом и анодом при токах, ограниченных пространственным зарядом?

8. Какова зависимость тока термоэмиссии от напряжения между анодом и катодом с учетом пространственного заряда и начальных скоростей электронов? Поясните смысл параметров, определяющих эту зависимость;

9. Объясните схему экспериментальной установки для изучения термоэлектронной эмиссии. Поясните назначение отдельных элементов схемы.

10. Объясните метод экспериментального определения показателя степени в законе "трех вторых".

9. Лабораторная работа №2. Изучение термоэлектронной эмиссии при малых плотностях эмиссионного тока

Цель работы: исследование вольт-амперной характеристики термодиода при малом токе накала катода. Определение из экспериментальных результатов контактной разности потенциалов между катодом и анодом, температуры катода.

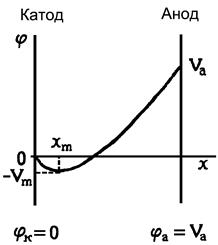
При малых плотностях термотока вольт-амперная характеристика имеет характерный вид с точкой перегиба, соответствующей модулю контактной разности потенциалов между катодом и анодом (рис. 10). Температуру катода можно определить следующим образом. Перейдем в уравнении (12) описывающем вольт-амперную характеристику термоэлектронной эмиссии при малых плотностях тока, от плотности термотока j к его полному значению I (j=I/S, где S – площадь поперечного сечения термотока). Тогда получим

, (35)

где I_S – ток насыщения.

Логарифмируя (35), имеем

. (36)

Постольку уравнение (36) описывает вольт-амперную характеристику на участке левее точки перегиба, то для определения температуры катода необходимо взять любые две точки на этом участке с анодными токами I_a₁, I_a₂и анодными напряжениями U_a₁, U_a₂ соответственно. Тогда, согласно уравнению (36),

Отсюда для температуры катода получим рабочую формулу

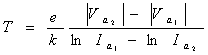. (37)

Порядок выполнения работы

Для выполнения лабораторной работы необходимо:

1. Ознакомиться с описанием и порядком работы с приборами, необходимыми для работы экспериментальной установки. Собрать схему согласно рис. 18. Установку можно включать в сеть только после проверки правильности собранной схемы инженером или преподавателем.

2. Включить источник питания тока накала катода и установит, требуемый ток накала. После установки тока необходимо выждать приблизительно 5 мин., чтобы ток накала и температура катода стабилизировались.

4. Результаты измерений представить на графике в координатах ln I_a(V_a), где I_a – анодный ток, V_a – анодное напряжение. Поскольку в данной работе контактная разность потенциалов определяется графическим методом, масштаб по горизонтальной оси следует выбрать таким образом, чтобы точность определения V_К.Р.П была не меньше 0,1 В.

5. По точке перегиба вольт-амперной характеристики определить контактную разность потенциалов между анодом и катодом.

6. Определить температуру катода для трех пар точек на наклонном линейном участке вольт-амперной характеристики левее точки перегиба. Температуру катода следует вычислять по формуле (37). Вычислить среднее значение температуры из этих данных.

7. Оформить отчет по работе.

Требования к отчету

Отчет оформляется на стандартном листе бумаги формата А4 и должен содержать:

1. Основные сведения по теории.

2. Схему экспериментальной установки и ее краткое описание.

3. Результаты измерений и расчетов.

4. Анализ полученных экспериментальных результатов.

5. Выводы по работе.

Контрольные вопросы

1. Перечислите виды эмиссии электронов. Что является причиной выхода электронов в каждом виде электронной эмиссии?

2. Объясните явление термоэлектронной эмиссии. Дайте определение работы выхода электрона из твердого тела. Как можно объяснить существование потенциального барьера на границе твердое тело – вакуум?

4. Сформулируйте закон Ричардсона-Дешмана. Объясните физический смысл входящих в этот закон величин.

5. В чем особенности вольт-амперной характеристики термокатода при малых плотностях тока эмиссии? Как влияет на нее контактная разность потенциалов между катодом и анодом?

6. В чем заключается эффект Шоттки? Как объясняется этот эффект?

7. Объясните понижение потенциального барьера для электронов под влиянием электрического поля.

8. Как определится температура катода в данной лабораторной работе?

9. Объясните метод определения контактной разности потенциалов в данной работе.

10. Объясните схему и назначение отдельных элементов лабораторной установки.